Cho \(\widehat{xOy}\) khác góc bẹt. Trên tia Ox lần lượt lấy 2 điểm B và C, trên tia Oy lần lượt lấy 2 điểm A và D sao cho OA=OB, OD=OC. GỌi I là giao điểm của AC và BD. Chứng minh:
a)\(\Delta OAC=\Delta OBD\)
b) IA=IB
c) OI là tia phân giác của \(\widehat{xOy}\)

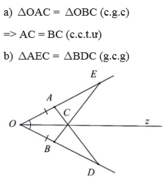
Hình vẽ :
a) Xét \(\Delta OACvà\Delta OBD\) là :
\(\left\{{}\begin{matrix}OA=OB\left(gt\right)\\\widehat{O}:chung\\OD=OC\left(gt\right)\end{matrix}\right.\)
=> \(\Delta OAC=\Delta OBD\left(c.g.c\right)\)
b) Ta có : \(\left\{{}\begin{matrix}OB=OA\\OC=OD\end{matrix}\right.\left(giảthiết\right)\)
Lại có : \(\left\{{}\begin{matrix}OC=OB+BC\\OD=OA+AD\end{matrix}\right.\)
Suy ra : \(\Rightarrow OC-OB=OD-OA\)
=> BC = AD
Xét \(\Delta IBCvà\Delta IAD\) có :
\(\left\{{}\begin{matrix}BC=AD\left(cmt\right)\\\widehat{BIC}=\widehat{AID}\left(đ.đỉnh\right)\\\widehat{ICB}=\widehat{IDA}\left(\Delta OAC=\Delta OBD\right)\end{matrix}\right.\)
=> \(\Delta IBC=\Delta IAD\left(g.c.g\right)\)
=> IA = IB (2 cạnh tương ứng)
c) Xét \(\Delta OBIvà\Delta OAI\) có :
\(\left\{{}\begin{matrix}OA=OB\left(gt\right)\\OI:chung\\AI=BI\left(câub\right)\end{matrix}\right.\)
=> \(\Delta OBI=\Delta OAI\left(c.c.c\right)\)
=> \(\widehat{IOB}=\widehat{IOA}\) (2 góc tương ứng)
=> OI là tia phân giác của góc xOy.
a: Xét ΔOAC và ΔOBD có
OA=OB
góc O chung
OC=OD
Do đo: ΔOAC=ΔOBD
b: Xét ΔIBC và ΔIAD có
góc IBC=góc IAD
BC=AD
góc ICB=góc IDA
Do đó: ΔIBC=ΔIAD
Suy ra: IB=IA
c: Xét ΔOIC và ΔOID có
OI chung
IC=ID
OC=OD
Do đó: ΔOIC=ΔOID
Suy ra: góc COI=góc DOI
hay OI là phân giác của góc xOy