Hai vật chuyển động thẳng đều trên cùng một đường thẳng. Nếu chúng chuyển động lại gần nhau thì cứ sau 5 giây khoảng cách giữa chúng giảm 8 m. Nếu chúng chuyển động cùng chiều (độ lớn vận tốc như cũ) thì cứ sau 10 giây khoảng cách giữa chúng lại tăng thêm 6m. Tính vận tốc của mỗi vật.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 5 2016
Gọi S1, S2 là quãng đường đi được của các vật,
v1,v2 là vận tốc vủa hai vật.
Ta có: S1 =v1t2 , S2= v2t2
Khi chuyển động lại gần nhau độ giảm khoảng cách của hai vật bằng tổng quãng đường hai vật đã đi: S1 + S2 = 8 m
S1 + S2 = (v1 + v2) t1 = 8
\(\Rightarrow\)v1 + v2 = \(\frac{S_1+S_2}{t_1}\) = \(\frac{5}{8}\) = 1,6 (1)
- Khi chúng chuyển động cùng chiều thì độ tăng khoảng cách giữa hai vật bằng hiệu quãng đường hai vật đã đi: S1 - S2 = 6 m
S1 - S2 = (v1 - v2) t2 = 6
\(\Rightarrow\)v1 - v2 = \(\frac{S_1-S_2}{t_1}\) = \(\frac{6}{10}\) = 0,6 (2)
Lấy (1) cộng (2) vế với vế ta được 2v1 = 2,2 \(\Leftrightarrow\)v1 = 1,1 m/s
Vận tốc vật thứ hai: v2 = 1,6 - 1,1 = 0,5 m/s
NE
2 tháng 10 2016
Bạn Lại Thị Hồng Liên làm ơn cho mình hỏi ngu xíu: có phải là:
- khi hai vật chuyển động ngược chiều thi độ TĂNG và cả GIẢM khoảng cách giữa hai vật đều bằng tổng quãng đường hai vật đi được
- khi chuyển động ngược chiều thì cả độ TĂNG hay GIẢM khoảng cách giữa hai vật đều bằng hiệu quãng đường hai vật đã đi?
Cảm ơn bạn nha!!!
13 tháng 6 2016
ta có:
v1+v2=8/5
\(\Leftrightarrow v_1+v_2=1.6\)(1)
nếu vận tốc xe một lớn hơn xe hai thì:
v1-v2=6/10=0.6(2)
giải một và hai ta có:v1=1.1;v2=0.5
nếu vận tốc xe hai lớn hơn xe một thì v1=0.5;v2=1.1
27 tháng 9 2021
1 phút = 60s
1km=1000m
a) Khi chuyển động ngược chiều:
Giả sử \(v_1>v_2\)
\(\Delta s_1=s_1+s_2\\ \Leftrightarrow\Delta s_1=v_1t+v_2t\\ \Leftrightarrow330=60v_1+60v_2\\ \Leftrightarrow v_1+v_2=5,5\left(1\right)\)
Khi chuyển động cùng chiều:
\(\Delta s_2=s_1-s_2\\ \Leftrightarrow\Delta s_2=v_1t'-v_2t'\Leftrightarrow25=10v_1-10v_2\\ \Leftrightarrow v_1-v_2=2,5\left(2\right)\)
\(\xrightarrow[\left(2\right)]{\left(1\right)}\left\{{}\begin{matrix}v_1=4\left(m/s\right)\\v_2=1,5\left(m/s\right)\end{matrix}\right.\)
b) Gọi t là thời gian 2 vật gặp khi đi ngược chiều
\(s=s_1+s_2\Leftrightarrow1000=4t+1,5t\\ \Leftrightarrow5,5t=1000\\ \Leftrightarrow t=\dfrac{2000}{11}\left(s\right)\)
Vị trí gặp cách điểm xuất phát của vật 1:
\(s_1=4.\dfrac{2000}{11}=\dfrac{8000}{11}\left(km\right)\)
Gọi t' là thời gian 2 vật gặp nhau khi đi cùng chiều:
\(s=s_1-s_2\\ \Leftrightarrow s=v_1t'-v_2t'\\ \Leftrightarrow1000=4t-1,5t\\ \Leftrightarrow1000=2,5t\\ \Leftrightarrow t=400\left(s\right)\)
Vị trí gặp cách điểm xuất phát của vật thứ nhất là:
\(s_1=4.400=1600\left(m\right)\)
CM
23 tháng 8 2018
Gọi vận tốc của hai vật lần lượt là x (cm/s) và y (cm/s)
Điều kiện x , y > 0.
Chu vi vòng tròn là : 20.π (cm)
Khi chuyển động cùng chiều, cứ 20 giây chúng lại gặp nhau, nghĩa là quãng đường 2 vật đi được trong 20 giây chênh lệch nhau đúng bằng 1 vòng tròn
⇒ Ta có phương trình: 20x – 20y = 20π.
Khi chuyển động ngược chiều, cứ 4 giây chúng lại gặp nhau, nghĩa là tổng quãng đường hai vật đi được trong 4 giây là đúng 1 vòng tròn
⇒ Ta có phương trình: 4x + 4y = 20π.
Ta có hệ phương trình:
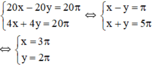
Vậy vận tốc của hai vật là 3π cm/s, 2π cm/s.
Chú ý : Chu vi đường tròn bán kính R là : P= 2πR= πd trong đó d là đường kính của đường tròn.
Kiến thức áp dụng
Giải bài toán bằng cách lập hệ phương trình :
Bước 1 : Lập hệ phương trình
- Chọn các ẩn số và đặt điều kiện thích hợp
- Biểu diễn các đại lượng chưa biết và đã biết theo ẩn
- Lập các phương trình biểu thị mối quan hệ giữa các đại lượng theo đề bài.
- Từ các phương trình vừa lập rút ra được hệ phương trình.
Bước 2 : Giải hệ phương trình (thường sử dụng phương pháp thế hoặc cộng đại số).
Bước 3 : Đối chiếu nghiệm với điều kiện và kết luận.
CM
18 tháng 6 2017
Gọi vận tốc của hai vật lần lượt là x (cm/s) và y (cm/s)
Điều kiện x , y > 0.
Chu vi vòng tròn là : 20.π (cm)
Khi chuyển động cùng chiều, cứ 20 giây chúng lại gặp nhau, nghĩa là quãng đường 2 vật đi được trong 20 giây chênh lệch nhau đúng bằng 1 vòng tròn
⇒ Ta có phương trình: 20x – 20y = 20π.
Khi chuyển động ngược chiều, cứ 4 giây chúng lại gặp nhau, nghĩa là tổng quãng đường hai vật đi được trong 4 giây là đúng 1 vòng tròn
⇒ Ta có phương trình: 4x + 4y = 20π.
Ta có hệ phương trình:
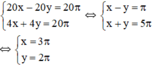
Vậy vận tốc của hai vật là 3π cm/s, 2π cm/s.
Chú ý : Chu vi đường tròn bán kính R là : P= 2πR= πd trong đó d là đường kính của đường tròn.
VT
26 tháng 7 2018
Giải:
Ta có t 1 = 30 p h = 1 3 h ; t 2 = 10 p h = 1 6 h
Chọn chiều dương là chiều chuyển động của mỗi xe.
Nếu đi ngược chiều thì S 1 + S 2 = 30
⇒ v 1 + v 2 t 1 = v 1 + v 2 1 3 = 30 ⇒ v 1 + v 2 = 90 ( 1 )
Nếu đi cùng chiều thì s 1 − s 2 = 10
⇒ v 1 − v 2 t 2 ⇒ v 1 − v 2 6 = 10 ⇒ v 1 − v 2 = 60 (2)
Giải (1) (2) v 1 = 75 k m / h ; v 2 = 15 k m / h
HH
30 tháng 9 2020
Gọi vận tốc của hai vật lần lượt là : x ( cm/s ) ; y ( cm/s )
Điều kiện : x , y > 0
Chu vi vòng tròn là : \(20.\pi\left(cm\right)\)
Khi chuyển động cùng chiều , cứ 20 giây chúng lại gặp nhau . Nghĩa là quãng đường 2 vật đi được trong 20s chênh lệch nhau đúng bằng 1 vòng tròn
=> Ta có PT : \(20x-20y=20\pi\)
Khi chuyển động ngược chiều , cứ 4 giây là chúng lại gặp nhau . Nghĩa là tổng quãng đường đi được trong 4 giây đúng là 1 vòng tròn .
=> Ta có PT : \(4x+4y=20\pi\)
Ta có HPT : \(\hept{\begin{cases}20x-20y=20\pi\\4x+4y=20\pi\end{cases}}\Leftrightarrow\hept{\begin{cases}x-y=\pi\\x+y=5\pi\end{cases}\Leftrightarrow}\hept{\begin{cases}x=3\pi\\y=2\pi\end{cases}}\)
Vậy vận tốc của hai vật là : \(3\pi/s\); \(2\pi/s\)
DD
Đỗ Duy Phong
VIP
30 tháng 9 2020
n.gjmlgb,g.gtlf[y[rtlkyf;hk/, lơpu]tup[ươt[jnlgngkjko8769=89065
Gọi v1 , v2 lần lượt là vận tốc của vật 1 và 2
Cứ sau 5 s khoảng cách của chúng giảm 8 m nên ta có pt :
5 (v1 + v2 ) = 8
=> v1 + v2 = \(\dfrac{8}{5}\) = 1,6 (1)
Cứ sau 10 s khoảng cách của chúng tăng 6 m nên ta có pt :
10 (v1 - v2 ) = 6
=> v1 - v2 = \(\dfrac{6}{10}\) = 0,6 (2)
Từ (1) vả (2) , ta tính được :
v1 = 1,1 ( m/s )
v2 = 0,5 (m/s)
Vậy vận tốc ...........
Câu hỏi của Đặng Minh Quân - Vật lý lớp 0 | Học trực tuyến