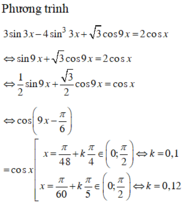Giải phương trình: \(3sin3x-\sqrt{3}cos9x=1+4sin^33x\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NC
1
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 9 2020
\(3sin3x-4sin^33x+\sqrt{3}sin9x=1\)
\(\Leftrightarrow sin9x+\sqrt{3}sin9x=1\)
\(\Leftrightarrow\left(\sqrt{3}+1\right)sin9x=1\)
\(\Leftrightarrow sin9x=\frac{1}{\sqrt{3}+1}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{1}{9}arcsin\left(\frac{1}{\sqrt{3}+1}\right)+k2\pi\\x=\pi-\frac{1}{9}arcsin\left(\frac{1}{\sqrt{3}+1}\right)+k2\pi\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 10 2020
Câu 1:
\(cos^2\) gì nhỉ?
Câu 2: đề không hợp lý \(\sqrt{3}sin9x\) là \(\sqrt{3}cos9x\) có lý hơn
\(\Leftrightarrow3sin3x-4sin^33x+\sqrt{3}sin9x=1\)
\(\Leftrightarrow sin9x+\sqrt{3}sin9x=1\)
\(\Leftrightarrow sin9x=\frac{1}{\sqrt{3}+1}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{1}{9}arcsin\left(\frac{1}{\sqrt{3}+1}\right)+\frac{k2\pi}{9}\\x=\frac{\pi}{9}-\frac{1}{9}arcsin\left(\frac{1}{\sqrt{3}+1}\right)+\frac{k2\pi}{9}\end{matrix}\right.\)
Nghiệm nhìn rất ngớ ngẩn nếu đề đúng
3.
\(\Leftrightarrow\frac{1}{2}-\frac{1}{2}cos2x+\frac{\sqrt{3}}{2}sin2x=1\)
\(\Leftrightarrow sin\left(2x-\frac{\pi}{6}\right)=\frac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\frac{\pi}{6}=\frac{\pi}{6}+k2\pi\\2x-\frac{\pi}{6}=\frac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow...\)
MA
1
HP
17 tháng 8 2021
\(4sin^2x.cosx+2cos2x=cosx+\sqrt{3}sin3x\)
\(\Leftrightarrow2\left(1-cos2x\right).cosx+2cos2x=cosx+\sqrt{3}sin3x\)
\(\Leftrightarrow2cosx-2cos2x.cosx+2cos2x=cosx+\sqrt{3}sin3x\)
\(\Leftrightarrow2cosx-cos3x-cosx+2cos2x=cosx+\sqrt{3}sin3x\)
\(\Leftrightarrow\sqrt{3}sin3x+cos3x=2cos2x\)
\(\Leftrightarrow\dfrac{\sqrt{3}}{2}sin3x+\dfrac{1}{2}cos3x=cos2x\)
\(\Leftrightarrow cos\left(3x-\dfrac{\pi}{3}\right)=cos2x\)
\(\Leftrightarrow3x-\dfrac{\pi}{3}=\pm2x+k2\pi\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=\dfrac{\pi}{15}+\dfrac{k2\pi}{5}\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 7 2021
1a.
Đặt \(5x+6=u\)
\(cos2u+4\sqrt{2}sinu-4=0\)
\(\Leftrightarrow1-2sin^2u+4\sqrt{2}sinu-4=0\)
\(\Leftrightarrow2sin^2u-4\sqrt{2}sinu+3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinu=\dfrac{3\sqrt{2}}{2}>1\left(loại\right)\\sinu=\dfrac{\sqrt{2}}{2}\end{matrix}\right.\)
\(\Rightarrow sin\left(5x+6\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}5x+6=\dfrac{\pi}{4}+k2\pi\\5x+6=\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{6}{5}+\dfrac{\pi}{20}+\dfrac{k2\pi}{5}\\x=-\dfrac{6}{5}+\dfrac{3\pi}{20}+\dfrac{k2\pi}{5}\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 7 2021
1b.
Đặt \(2x+1=u\)
\(cos2u+3sinu=2\)
\(\Leftrightarrow1-2sin^2u+3sinu=2\)
\(\Leftrightarrow2sin^2u-3sinu+1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinu=1\\sinu=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(2x+1\right)=1\\sin\left(2x+1\right)=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+1=\dfrac{\pi}{2}+k2\pi\\2x+1=\dfrac{\pi}{6}+k2\pi\\2x+1=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}+\dfrac{\pi}{4}+k\pi\\x=-\dfrac{1}{2}+\dfrac{\pi}{12}+k\pi\\x=-\dfrac{1}{2}+\dfrac{5\pi}{12}+k\pi\end{matrix}\right.\)