Tam giac ABC co AB=a,AC=b AD la duong phan giac,AM la duong trung tuyen,D la trung diem MN, N thuoc BC.Tinh BN/NC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VM
23 tháng 9 2019
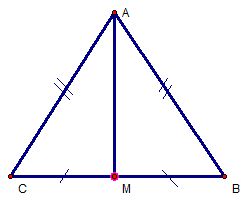
a) Xét 2 \(\Delta\) \(ABM\) và \(ACM\) có:
\(AB=AC\left(gt\right)\)
\(BM=CM\) (vì M là trung điểm của \(BC\))
Cạnh AM chung
=> \(\Delta ABM=\Delta ACM\left(c-c-c\right)\)
=> \(\widehat{BAM}=\widehat{CAM}\) (2 góc tương ứng)
=> \(AM\) là đường phân giác của \(\widehat{A}.\)
b) Xét \(\Delta ABC\) có:
\(AB=AC\left(gt\right)\)
=> \(\Delta ABC\) cân tại A.
Có \(AM\) là đường phân giác (cmt) đồng thời \(AM\) cũng là đường cao của \(\Delta ABC.\)
=> \(AM\) là đường cao của \(\Delta ABC.\)
c) Theo câu b) ta có \(\Delta ABC\) cân tại A.
Có \(AM\) là đường cao đồng thời \(AM\) cũng là đường trung trực của \(\Delta ABC.\)
=> \(AM\) là đường trung trực của \(BC.\)
Chúc bạn học tốt!
20 tháng 7 2019
Ta thấy AM là trung tuyến
=> BM = MC
Trong ∆ vuông ABC có AM là trung tuyến
=> AM = \(\frac{1}{2}\)BC
=> AM = BM = CM
=> AM = CM
=> ∆AMC cân tại M
Mà ∆ ABC có MN là trung tuyến
=> MN là trung trực ∆AMC
=> MN vuông góc với AC
Vì AM = \(\frac{1}{2}\)BC
=> 2AM = BC (dpcm)