Cho hàm số y=-x^{3}+3x^{2}-5. Khẳng định nào dưới đây là đúng?
- Hàm số đồng biến trên (0;2), nghịch biến trên (-\infty;0) và (2;+\infty)
- Hàm số đồng biến trên (-\infty;0) và (2;+\infty), nghịch biến trên (0;2)
- Hàm số đồng biến trên (-1;2), nghịch biến trên (-\infty;-1) và (2;+\infty)
- Hàm số đồng biến trên (-\infty;-1) và (2;+\infty),nghịch biến trên (-1;2)

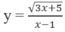 xác định trên R
xác định trên R


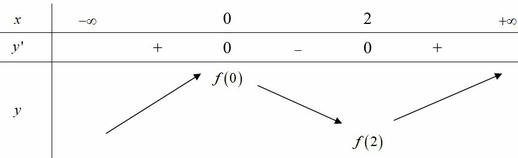

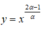
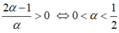
Lời giải:
Ta có:
\(y'=-3x^2+6x\)
\(y'>0\Leftrightarrow -3x^2+6x>0\Leftrightarrow 0< x< 2\) (khoảng đồng biến)
\(y'< 0\Leftrightarrow -3x^2+6x< 0\Leftrightarrow x<0\) hoặc \(x>2\), tức là \(x\in (-\infty, 0)\) hoặc \(x\in (2;+\infty)\) (khoảng nghịch biến)
Từ đây ta suy ra A là đáp án đúng.