Question

[Phuong Tran]

cho tam giác ABC. kẻ phân giác trong BD, CK. từ A kẻ đường thẳng vuông góc với CK tại M, từ A, C kẻ các đường thẳng vuông góc với BD tại N và L tương ứng, MN cắt AC tại E, BF cắt CL tại E

a, chứng minh MN//BC

b, chứng minh LF//AB và LF đi qua trung điểm BC

c, chứng minh DE//BC

Answer 1

[Ngô Kim Tuyền]

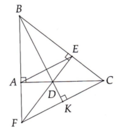
a) AM cắt BC tại P, AN cắt BC tại Q

Ta có: BN là đường cao của \(\Delta ABQ\) (gt) (1)

Mà BD là đường phân giác của \(\Delta ABC\) (gt)

\(\Rightarrow BN\)cũng là đường phân giác của \(\Delta ABQ\left(2\right)\)

Từ (1), (2) \(\Rightarrow\Delta ABQ\) cân tại B (3)

Từ (1), (3) \(\Rightarrow BN\) cũng là đường trung tuyến của \(\Delta ABQ\)

\(\Rightarrow\) NA = NQ (4)

Tương tự có: CM là đường cao của \(\Delta ACP\) (gt) (5)

Mà CK là đường phân giác của \(\Delta ABC\)

\(\Rightarrow CM\)cũng là đường phân giác của \(\Delta ACP\)(6)

Từ (5), (6) \(\Rightarrow\Delta ACP\) cân tại C (7)

Từ (6), (7) \(\Rightarrow CM\)cũng là đường trung tuyến của \(\Delta ACP\)

\(\Rightarrow MA=MP\left(8\right)\)

Từ (4), (8) \(\Rightarrow MN\)là đường trung bình của \(\Delta APQ\)

\(\Rightarrow MN\)// PQ

\(\Rightarrow MN\)// BC (9)

b) MF cắt LC tại H

Từ (9) \(\Rightarrow\) MF // PC (10)

Từ (8), (10) \(\Rightarrow FA=FC\) (11)

Từ (1) \(\Rightarrow\) BN \(\perp AQ\)

\(\Rightarrow BL\perp AQ\) (12)

Mà BL \(\perp LC\) (gt) (13)

Từ (12), (13) \(\Rightarrow AQ\) // LC

\(\Rightarrow\widehat{NAF}=\widehat{HCF}\) (2 góc so le trong) (14)

Xét \(\Delta NFA\) và \(\Delta HFC\) ta có:

\(\widehat{NFA}=\widehat{HFC}\) (2 góc đối đỉnh) (15)

Từ (11), (14), (15) \(\Rightarrow\Delta NFA=\Delta HFC\left(G-C-G\right)\)

\(\Rightarrow FN=FH\) (2 cạnh tương ứng) (16)

Từ (16) \(\Rightarrow LF\) là đường trung tuyến ứng với cạnh huyền NH của \(\Delta NLH\) vuông tại L

\(\Rightarrow LF=\dfrac{1}{2}NH\) (17)

Từ (16) \(\Rightarrow FN=FH=\dfrac{1}{2}NH\) (18)

Từ (17), (18) \(\Rightarrow LF=FN\)

\(\Rightarrow\Delta LFN\) cân tại F

\(\Rightarrow\)\(\widehat{LNF}=\widehat{NLF}\) (19)

Từ (2) \(\Rightarrow\widehat{ABN}=\widehat{QBN}\) (20)

Từ (9) \(\Rightarrow\widehat{MNB}=\widehat{QBN}\) (2 góc so le trong) (21)

Từ (20), (21) \(\Rightarrow\) \(\widehat{ABN}=\widehat{MNB}\) (22)

Mà \(\widehat{LNF}=\widehat{MNB}\) (2 góc đối đỉnh) (23)

Từ (22), (23) \(\Rightarrow\widehat{ABN}=\widehat{LNF}\left(24\right)\)

Từ (19), (24) \(\Rightarrow\widehat{NLF}=\widehat{ABN}\) (25)

Mà đây là cặp góc ở vị trí so le trong

\(\Rightarrow LF\) // AB

LF cắt BC tại G

Từ (20), (25) \(\Rightarrow\Delta BGL\) cân tại G

\(\Rightarrow GB=GL\) (26)

Từ (9) \(\Rightarrow MH\)// PC

\(\Rightarrow\widehat{LHF}=\widehat{LCG}\) (2 góc đồng vị) (27)

Từ (17), (18) \(\Rightarrow LF=FH\)

\(\Rightarrow\Delta LFH\) cân tại F

\(\Rightarrow\widehat{HLF}=\widehat{LHF}\) (28)

Từ (27), (28) \(\Rightarrow\widehat{LCG}=\widehat{HLF}\)

\(\Rightarrow\Delta LGC\) cân tại G

\(\Rightarrow GL=GC\) (29)

Từ (26), (29) \(\Rightarrow GB=GC\)

Vậy LF sẽ đi qua trung điểm của BC

c) Từ (9) \(\Rightarrow\) NF // BC (30)

Từ (30), theo hệ quả của định lý Ta-lét ta có:

\(\dfrac{ND}{BD}=\dfrac{FN}{BC}\) (31)

Từ (30) \(\Rightarrow FG\)// BC, theo hệ quả của định lý Ta-lét ta có:

\(\dfrac{EF}{EB}=\dfrac{FH}{BC}\) (32)

Từ (16) \(\Rightarrow\dfrac{FN}{BC}=\dfrac{FH}{BC}\) (33)

Từ (31), (32), (33) \(\Rightarrow\dfrac{ND}{BD}=\dfrac{EF}{EB}\) (34)

Từ (34) \(\Rightarrow\) NF // DE (định lý Ta-lét đảo) (35)

Từ (30), (35) \(\Rightarrow DE\) // BC