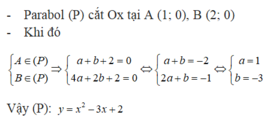Tập hợp đỉnh y của parabol y=x^2-2mx+2m^2-4m+3 là parabol (Q). Parabol (Q) có thể cắt trục hoành tại điểm nào sau đây?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 6 2021
a) Thay x=1 và y=-2 vào (P), ta được:
\(a\cdot1^2-4\cdot1+c=-2\)
\(\Leftrightarrow a-4+c=-2\)
hay a+c=-2+4=2
Thay x=2 và y=3 vào (P), ta được:
\(a\cdot2^2-4\cdot2+c=3\)
\(\Leftrightarrow4a-8+c=3\)
hay 4a+c=11
Ta có: \(\left\{{}\begin{matrix}a+c=2\\4a+c=11\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-3a=-9\\a+c=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=3\\c=2-a=2-3=-1\end{matrix}\right.\)
Vậy: (P): \(y=3x^2-4x-1\)
19 tháng 2 2021
Em nghĩ nên sửa đề thành Parabol đi qua điểm (3;3) thì bài toán mới giải được ạ
Parabol đi qua điểm (3;3) nên ta có:
\(3=\left(2m-1\right)\cdot3^2\Rightarrow2m-1=\frac{1}{3}\)
\(\Leftrightarrow2m=\frac{4}{3}\Rightarrow m=\frac{2}{3}\)
Khi đó ta được parabol \(y=\frac{x^2}{3}\)
Đường thẳng song song với trục hoành cắt trục tung tại điểm có tung độ là 4 => y = 4
Khi đó \(4=\frac{x^2}{3}\Rightarrow x^2=12\Rightarrow\orbr{\begin{cases}x=2\sqrt{3}\\x=-2\sqrt{3}\end{cases}}\)
G/s A nằm ở phía dương, B ở phía âm đối với trục hoành thì khi đó tọa độ của A và B là: \(\hept{\begin{cases}A\left(2\sqrt{3};4\right)\\B\left(-2\sqrt{3};4\right)\end{cases}}\)
\(\Rightarrow AB=\left|2\sqrt{3}\right|+\left|-2\sqrt{3}\right|=4\sqrt{3}\)
\(\Rightarrow S_{OAB}=\frac{4\sqrt{3}\cdot4}{2}=8\sqrt{3}\left(dvdt\right)\)
VH
12 tháng 10 2020
Đỉnh của parabol là \(\frac{-\Delta}{4a}\) ta có
\(\left\{{}\begin{matrix}\frac{-\Delta}{4a}=-25\\16a-4b+c=0\\36a+6b+c=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b^2-4ac=100a\\16a-4b+c=0\\36a+6b+c=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b^2-4ac=100a\\16a-4b+c=0\\36a+6b+c=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b^2-4ac=100a\\24a+c=0\\2a+b=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4a^2-4ac=100a\\24a+c=0\\b=-2a\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-c=25\\24a+c=0\\b=-2a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=-2\\c=-24\end{matrix}\right.\)
\(\Rightarrow y=x^2-2x-24\)
CM
1 tháng 3 2019
Vì parabol (P) cắt trục Ox tại điểm có hoành độ bằng 2 nên A(2; 0) thuộc (P).
Thay x = 0; y = 2 vào phương trình parabol ta được 0 = 4a + 6 – 2 hay a = -1
Chọn D.
BT
5 tháng 6 2017
Điều kiện để (P): \(y=ax^2+bx+c\) cắt trục hoành tại hai điểm phân biệt là \(\Delta>0\).
Gọi \(x_1;x_2\) là hoành độ của hai giao điểm. Ta có:
\(x_{1,2}=\dfrac{-b\pm\sqrt{\Delta}}{2a}\);
Tọa độ giao điểm là:
\(A\left(\dfrac{-b+\sqrt{\Delta}}{2a};0\right)\); \(A\left(\dfrac{-b-\sqrt{\Delta}}{2a};0\right)\).
