Giúp em bài cosi này với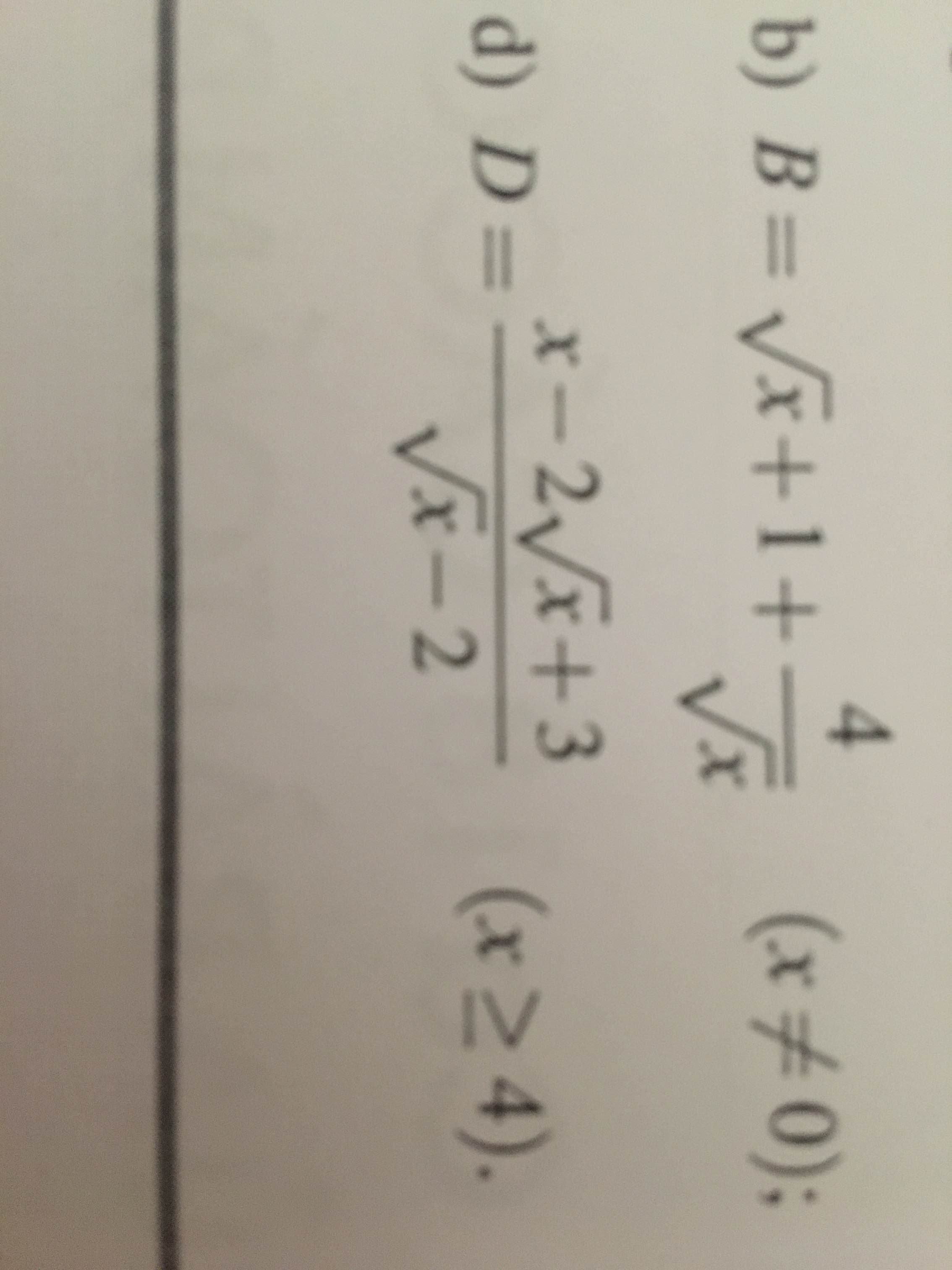 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 9 2021
c) Ta có: \(C=\dfrac{x+\sqrt{x}+1}{\sqrt{x}+1}=\sqrt{x}+\dfrac{1}{\sqrt{x}+1}=\left(\sqrt{x}+1\right)+\dfrac{1}{\sqrt{x}+1}-1\)
Áp dụng BĐT Cô-si ta có:
\(\sqrt{x}+1+\dfrac{1}{\sqrt{x}+1}\ge2\sqrt{\left(\sqrt{x}+1\right).\dfrac{1}{\sqrt{x}+1}}=2\)
\(\Rightarrow C\ge2-1=1\)
Dấu "=" xảy ra ⇔ \(\sqrt{x}+1=1\Leftrightarrow x=0\)
13 tháng 9 2021
a)
Ta có: \(A=\sqrt{x}-1+\dfrac{4}{\sqrt{x}-1}\ge2\sqrt{\left(\sqrt{x}-1\right).\dfrac{4}{\sqrt{x}-1}}=2\)
Dấu "=" xảy ra \(\Leftrightarrow\left(\sqrt{x}-1\right)^2=4\Leftrightarrow\sqrt{x}-1=2\Leftrightarrow x=9\)
20 tháng 8 2021
Nói thật với bạn mình không biết sử dụng BĐT Cô si cho dạng này, nhưng mình có một cách làm dễ hơn, bạn tham khảo nhé.
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 8 2021
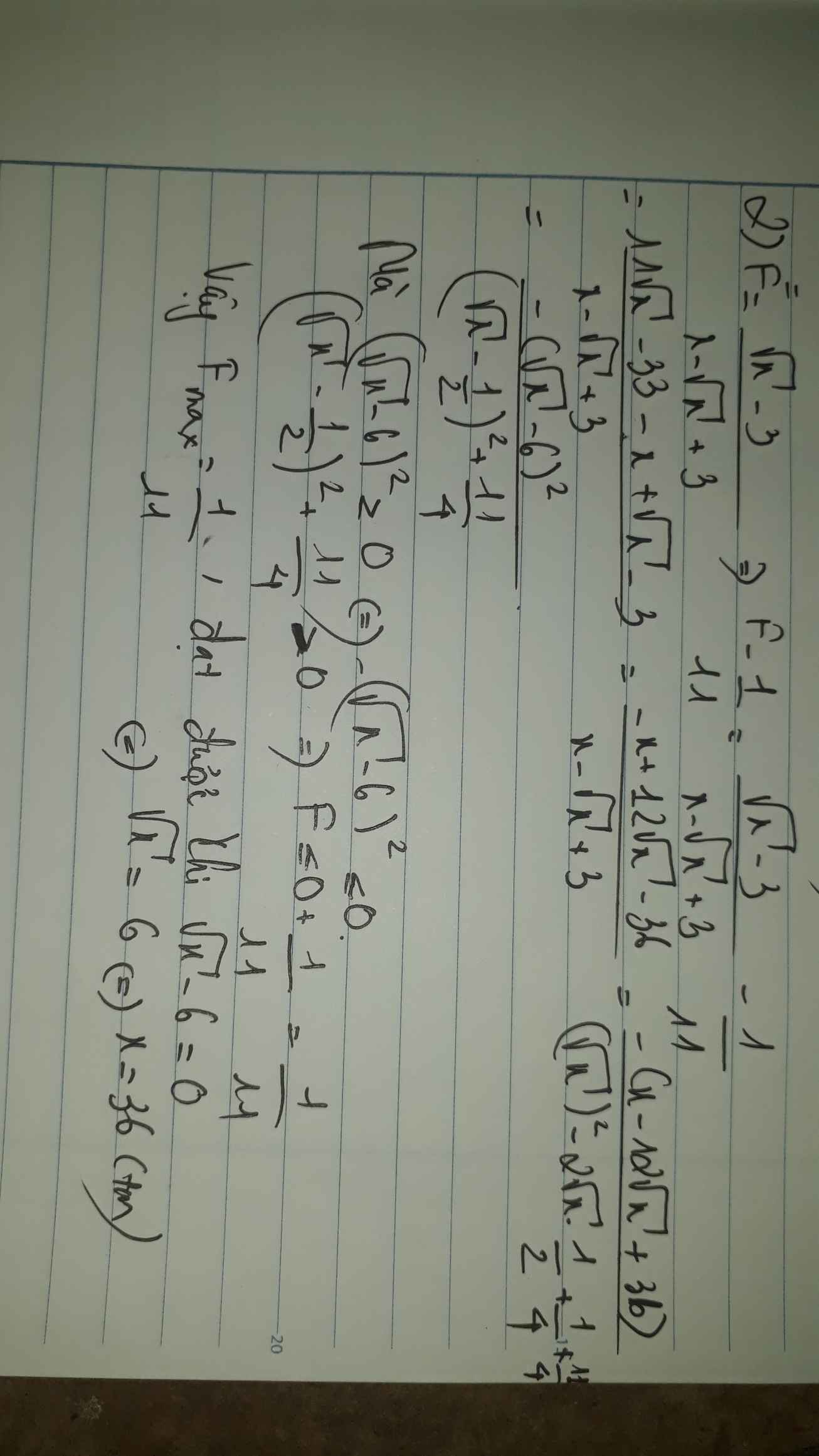
\(x>9\Rightarrow\sqrt{x}-3>0\Rightarrow F>0\)
\(\dfrac{1}{F}=\dfrac{x-\sqrt{x}+3}{\sqrt{x}-3}=\sqrt{x}+2+\dfrac{9}{\sqrt{x}-3}=\sqrt{x}-3+\dfrac{9}{\sqrt{x}-3}+5\ge2\sqrt{\dfrac{9\left(\sqrt{x}-3\right)}{\sqrt{x}-3}}+5=11\)
\(\Rightarrow F\le\dfrac{1}{11}\)
\(F_{max}=\dfrac{1}{11}\) khi \(\sqrt{x}-3=3\Rightarrow x=36\)
MN
1
TQ
13 tháng 10 2015
Áp dụng BĐT cô si cho 3 số không âm ta có:
\(\frac{4a+1+1}{2}\ge\sqrt{4a+1}\Leftrightarrow\frac{4a+2}{2}\ge\sqrt{4a+1}\Leftrightarrow2a+1\ge\sqrt{4a+1}\)
Mà a>0 nên: \(2a+1>\sqrt{4a+1}\)
Tương tự với \(\sqrt{4b+1}\) và \(\sqrt{4c+1}\) ta có:
\(2b+1>\sqrt{4b+1};2c+1>\sqrt{4c+1}\)
=>\(\sqrt{4a+1}+\sqrt{4b+1}+\sqrt{4c+1}<2a+1+2b+1+2c+1\)
\(=2.\left(a+b+c\right)+3=2.1+3=5\)
=>điều phải chứng minh
TL
1
KN
12 tháng 5 2021
a độ tụ của thấu kính là:
D=\(\dfrac{1}{f}=\dfrac{1}{-0,3}=\dfrac{-10}{3}\)
b. áp dụng công thức thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{d'}=\dfrac{1}{f}-\dfrac{1}{d}=\dfrac{1}{-30}-\dfrac{1}{20}=\dfrac{-1}{12}\Rightarrow d'=-12\)
tính chất của ảnh: là ảnh ảo ngược chiều
số phóng đại: k=\(\dfrac{-d'}{d}=\dfrac{-\left(-12\right)}{20}=\dfrac{3}{5}\)
độ cao của ảnh: A'B'=kAB<->A'B'=\(\dfrac{3}{5}\cdot5=3\)
Q
28 tháng 7 2021
lần đổ 1
\(\left(mC+m'C'\right).\left(38-20\right)=mC.\left(60-38\right)\)
\(\Leftrightarrow\left(mC+m'C'\right)18=mC.22\)
\(\Leftrightarrow2mC=9m'C'\)
lần 2 \(\left(2mC+m'C'\right)\left(t_x-38\right)=mC.\left(60-t_x\right)\)
\(11m'C'\left(t_x-38\right)=\dfrac{9}{2}.m'C'\left(60-t_x\right)\)
\(\Rightarrow t_x=...\)
21 tháng 8 2021
Bài 1:
a: Xét tứ giác NPIK có
\(\widehat{NKP}=\widehat{NIP}\left(=90^0\right)\)
Do đó: NPIK là tứ giác nội tiếp
hay N,P,I,K cùng thuộc 1 đường tròn
b: Xét tứ giác MKHI có
\(\widehat{MKH}+\widehat{MIH}=180^0\)
Do đó: MKHI là tứ giác nội tiếp
hay M,K,H,I cùng thuộc 1 đường tròn