tính chiều cao của một cây cổ thụ có bóng trên mặt đất dài 8m và có tia sáng từ đỉnh tạo với mặt đất một góc bằng 60 độ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 1
Gọi chân cột đèn là điểm A, đỉnh cột đèn là điểm B và bóng của đỉnh cột trên mặt đất là C
Ta có tam giác ABC vuông tại A với \(AC=7,5\left(m\right)\) và \(\widehat{BCA}=42^0\)
Trong tam giác vuông ABC:
\(AB=AC.tan\widehat{BAC}=7,5.tan42^0\approx6,8\left(m\right)\)
AD
30 tháng 10 2023
Đáp án: ≈12 mét
Giải thích các bước giải:
Chiều cao của cây là 20.tan31≈12mét
30 tháng 10 2023
\(\tan (C) = \dfrac{AB}{AC} \) ⇔ \(\tan (33) = \dfrac{AB}{40}\) ⇔ \(AB \) \(= 25,9 m\)
14 tháng 7 2023
7: ΔABC vuông tại A có AB=12m; góc B=52 độ. Tính AC
AC=AB*tan52=12*tan52=15,36(m)
AH
Akai Haruma
Giáo viên
29 tháng 7 2021
Bài 3:
Góc tạo bởi tia sáng với mặt đất là $\alpha$
Ta có:
$\tan \alpha=\frac{7}{4}\Rightarrow \alpha=60,26^0$
14 tháng 8 2023
1: Chiều cao của cột đèn là:
7,5*tan42\(\simeq6,75\left(m\right)\)
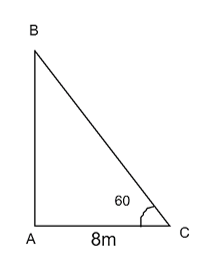
\(\tan\widehat{BCA}=\dfrac{AB}{AC}=\dfrac{AB}{8}\Rightarrow\tan60^o=\dfrac{AB}{8}\Rightarrow AB=8\sqrt{3}\left(cm\right)\)
là sao mình k hiểu