cho hai tam giác ABC và tam giác A'B'C' có chu vi bằng 15cm, biết AB=A'B'=3cm; AC=A'C'=7cm. CM: ∠A=∠A' ∠B=∠B' ∠C=∠C'
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét hai tam giác ABC và tam giác MNP có A ^ = M ^ , B ^ = N ^ .
Để hai tam giác ABC và MNP bằng nhau cần điều kiện A B = M N theo trường hợp góc – cạnh – góc .
Chọn đáp án B.

a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
góc BAD chung
=>ΔABD đồng dạng với ΔACE
=>AD/AE=AB/AC
=>AD*AC=AE*AB; AD/AB=AE/AC
b: Xet ΔADE và ΔABC có
AD/AB=AE/AC
góc DAE chung
=>ΔADE đồng dạng với ΔABC

a/ Ta có: \(\widehat{B}\)=\(\widehat{F}\); AB = EF
Để tam giác ABC = tam giác DEF theo trường hợp cạnh góc cạnh, ta cần bổ sung điều kiện BC = FD
Khi đó. tam giác ABC = tam giác EFD (c.g.c)
b/ Ta có: tam giác ABC = tam giác EFD
=> AB = EF; BC = FD; AC = DE
Chu vi tam giác ABC = tam giác EFD
AB + BC + AC = EF + FD + DE = 5 + 6 + 6
= 17 (cm)
Vậy chu vi tam giác ABC=chu vi tam giác EFD = 17 cm

Ta có: C ^ = P ^ mà góc C và góc P là hai góc nhọn kề của tam giác ABC và tam giác MNP
Do đó để tam giác ABC và tam giác MNP bằng nhau theo trường hợp cạnh góc vuông – góc nhọn kề thì cần thêm điều kiện A C = M P
Đáp án A

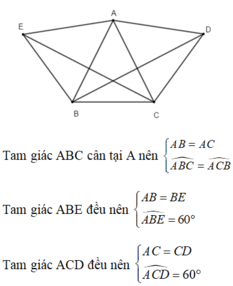
B'C'=BC=15-3-7=5(cm)
Xét ΔABC và ΔA'B'C' có
AB=A'B'
BC=B'C"
AC=A'C'
Do đó: ΔABC=ΔA'B'C'
Suy rA: góc A=góc A', góc B=góc B', góc C=góc C'