Rút gọn biểu thức (làm chi tiết các bước) theo như cô hướng dẫn
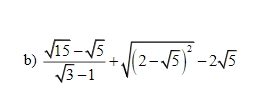
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(e,\left(5+2\sqrt{6}\right)\left(49-20\sqrt{6}\right)\sqrt{5-2\sqrt{6}}\\ =\left(5+2\sqrt{6}\right)\left(\sqrt{3}-\sqrt{2}\right)\left(5-2\sqrt{6}\right)^2\\ =\left(5-2\sqrt{6}\right)\left(\sqrt{3}-\sqrt{2}\right)\\ =\left(\sqrt{3}-\sqrt{2}\right)^2\left(\sqrt{3}-\sqrt{2}\right)=\left(\sqrt{3}-\sqrt{2}\right)^3\)
\(f,\left(2\sqrt{6}-4\sqrt{3}+5\sqrt{2}-\dfrac{1}{4}\sqrt{8}\right)\cdot3\sqrt{6}\\ =36-36\sqrt{2}+30\sqrt{3}-3\sqrt{3}=36-36\sqrt{2}+27\sqrt{3}\)
\(g,\left(2+\sqrt{3}-\sqrt{2}\right)\left(2-\sqrt{3}-\sqrt{2}\right)\left(3+\sqrt{2}\right)\sqrt{3-2\sqrt{2}}\\ =\left[\left(2-\sqrt{2}\right)^2-\left(\sqrt{3}\right)^2\right]\left(3+\sqrt{2}\right)\sqrt{\left(\sqrt{2}-1\right)^2}\\ =\left(3-4\sqrt{2}\right)\left(3+\sqrt{2}\right)\left(\sqrt{2}-1\right)\\ =\left(1-9\sqrt{2}\right)\left(\sqrt{2}-1\right)\\ =10\sqrt{2}-37\)
\(h,A=\sqrt{4+\sqrt{10+2\sqrt{5}}}+\sqrt{4-\sqrt{10+2\sqrt{5}}}\\ A^2=4+\sqrt{10+2\sqrt{5}}+4-\sqrt{10+2\sqrt{5}}+2\sqrt{\left(4+\sqrt{10+2\sqrt{5}}\right)\left(4-\sqrt{10+2\sqrt{5}}\right)}\\ A^2=8+2\sqrt{6-2\sqrt{5}}\\ A^2=8+2\left(\sqrt{5}-1\right)\\ A^2=6+2\sqrt{5}\\ A=\sqrt{6+2\sqrt{5}}=\sqrt{\left(\sqrt{5}+1\right)^2}=\sqrt{5}+1\)

\(b,\sqrt{15-\sqrt{216}}+\sqrt{33-12\sqrt{6}}\\ =\sqrt{15-6\sqrt{6}}+\sqrt{\left(2\sqrt{6}-3\right)^2}\\ =\sqrt{\left(3-\sqrt{6}\right)^2}+2\sqrt{6}-3\\ =3-\sqrt{6}+2\sqrt{6}-3=\sqrt{6}\)
\(c,\sqrt{2-\sqrt{3}}\left(\sqrt{6}+\sqrt{2}\right)\\ =\sqrt{12-6\sqrt{3}}+\sqrt{4-2\sqrt{3}}\\ =\sqrt{\left(3-\sqrt{3}\right)^2}+\sqrt{\left(\sqrt{3}-1\right)^2}\\ =3-\sqrt{3}+\sqrt{3}-1=2\)
c: \(\sqrt{2-\sqrt{3}}\cdot\left(\sqrt{6}+\sqrt{2}\right)\)
\(=\sqrt{4-2\sqrt{3}}\cdot\left(\sqrt{3}+1\right)\)
\(=\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)\)
=3-1
=2

Bước 1: Cắt tờ giấy thành một hình vuông

Bước 2: Gấp chéo tờ giấy lại như hình rồi mở lại để tạo thành nếp

Bước 3: Sau đó theo đường gấp vậy bạn gấp từ trái vào trong.

Bước 4: Sau đó các bạn quay lại 1 góc 90° bạn sẽ được thân con cá

Bước 5: Gấp chéo vào một góc để làm đuôi cá

Bước 6: Gấp ngược lại như hình trên sẽ được đuôi cá hoàn chỉnh


Ta có:\(x\left(x+y\right)+y\left(x-y\right)=x^2+xy+xy-y^2\)
\(=x^2+2xy-y^2\)
\(=-\left(x^2-2xy+y^2\right)+2x^2\)
Áp dụng hằng đẳng thức (a-b)2=a2-2ab+b2 ta đc:
\(=2x^2-\left(x-y\right)^2\)
Tại x = - 8 ; y = 7 ta đc:
\(=2\left(-8\right)^2-\left(-8-7\right)^2\)
\(=-241\)

\(\frac{1515}{2525}=\frac{15x101}{25x101}=\frac{3}{5}\)

a) Ta có: \(B=\sqrt{16x+16}-\sqrt{9x+9}+\sqrt{4x+4}+\sqrt{x+1}\)
\(=4\sqrt{x+1}-3\sqrt{x+1}+2\sqrt{x+1}+\sqrt{x+1}\)
\(=4\sqrt{x+1}\)
b) Để B=16 thì \(4\sqrt{x+1}=16\)
\(\Leftrightarrow x+1=16\)
hay x=15

\(a,=\dfrac{-\sqrt{a}\left(1-\sqrt{a}\right)}{1-\sqrt{a}}=-\sqrt{a}\\ b,=\dfrac{\sqrt{p}\left(\sqrt{p}-2\right)}{\sqrt{p}-2}=\sqrt{p}\)

a: \(=\dfrac{\left(3x-1\right)^3}{3x-1}\cdot\dfrac{8xy}{12x^3}=\dfrac{2y\left(3x-1\right)^2}{3x^2}\)
b: \(=\dfrac{\left(x-5\right)\left(x+5\right)}{x\left(x-5\right)}=\dfrac{x+5}{x}\)

\(\dfrac{4x^3+4x^2}{x^2-1}=\dfrac{4x^2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x^2}{x-1}\)
\(\dfrac{b^2+b}{a+ab}=\dfrac{b\left(b+1\right)}{a\left(b+1\right)}=\dfrac{b}{a}\)
d) Để phân thức \(\dfrac{4x^3+4x^2}{x^2-1}\) có nghĩa thì: \(x^2-1\ne0\Leftrightarrow x\ne\pm1\)
Khi đó: \(\dfrac{4x^3+4x^2}{x^2-1}=\dfrac{4x^2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x^2}{x-1}\)
e) Để phân thức \(\dfrac{b^2+b}{a+ab}\) có nghĩa thì: \(a+ab\ne0\Leftrightarrow a\ne-ab\)
Khi đó: \(\dfrac{b^2+b}{a+ab}=\dfrac{b\left(b+1\right)}{a\left(1+b\right)}=\dfrac{b}{a}\)
Ta có: \(\dfrac{\sqrt{15}-\sqrt{5}}{\sqrt{3}-1}+\sqrt{\left(2-\sqrt{5}\right)^2}-2\sqrt{5}\)
\(=\sqrt{5}+\sqrt{5}-2-2\sqrt{5}\)
=-2