Giúp mink câu 1 và câu 2 với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
C
31 tháng 10 2019
Câu 2
-Theo số liệu năm 2002 dân số Châu Á chiếm gần 61% dân số thế giới
-Dân số Châu Á ngày càng tăng
-Tỉ lệ gia tăng dân số tự nhiên cao ( 1,3% )
-Kế hoạch hóa gia đình còn thấp,kinh tế chủ yếu là nông nghiệp
Câu 1
Đặc điểm địa hình
-Dãy núi chính:Hy-ma-lay-a,Côn Luân,....
-Sơn nguyên:Trung Xi-bia,Tây Tạng,........
-Đồng bằng:Tu-ran,Lưỡng Hằng,......
-Châu Á có nhiều hệ thống núi,sơn nguyên cao,đồ sộ và nhiều đồng bằng rộng bậc nhất thế giới.
-Các dãy núi chạy theo 2 hướng chính:Bắc Nam,gần Bắc Nam,Đông Tây,gần Đông Tây.
=> Địa hình bị chia cắt rất phức tạp.
-Các núi và sơn nguyên cao tập trung ở vùng trung tâm.Trên các núi và sơn nguyên cao có băng hà bao phủ quanh năm.
Khoáng sản:
-Có nguồn khoáng sản phong phú,có trữ lượng lớn.
-Các khoáng sản quan trọng:dầu mỏ,khí đốt,......
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
28 tháng 12 2023
Câu 1: Vì p và 10p + 1 là các số nguyên tố lớn hơn 3 nên p ≠ 2 vậy p là các số lẻ.
Ta có: 10p + 1 - p = 9p + 1
Vì p là số lẻ nên 9p + 1 là số chẵn ⇒ 9p + 1 = 2k
17p + 1 = 8p + 9p + 1 = 8p + 2k = 2.(4p + k) ⋮ 2
⇒ 17p + 1 là hợp số (đpcm)
AH
Akai Haruma
Giáo viên
28 tháng 12 2023
Câu 1:
Vì $p$ là stn lớn hơn $3$ nên $p$ không chia hết cho $3$. Do đó $p$ có dạng $3k+1$ hoặc $3k+2$.
Nếu $p=3k+2$ thì:
$10p+1=10(3k+2)+1=30k+21\vdots 3$
Mà $10p+1>3$ nên không thể là số nguyên tố (trái với giả thiết)
$\Rightarrow p$ có dạng $3k+1$.
Khi đó:
$17p+1=17(3k+1)+1=51k+18=3(17k+6)\vdots 3$. Mà $17p+1>3$ nên $17p+1$ là hợp số
(đpcm)
4 tháng 9 2021
Bài 4:
a: Ta có: \(-\left|x+1.1\right|\le0\forall x\)
\(\Leftrightarrow-\left|x+1.1\right|+1.5\le1.5\forall x\)
Dấu '=' xảy ra khi x=-1,1
b: Ta có: \(-4\left|x-2\right|\le0\forall x\)
\(\Leftrightarrow-4\left|x-2\right|+10\le10\forall x\)
Dấu '=' xảy ra khi x=2
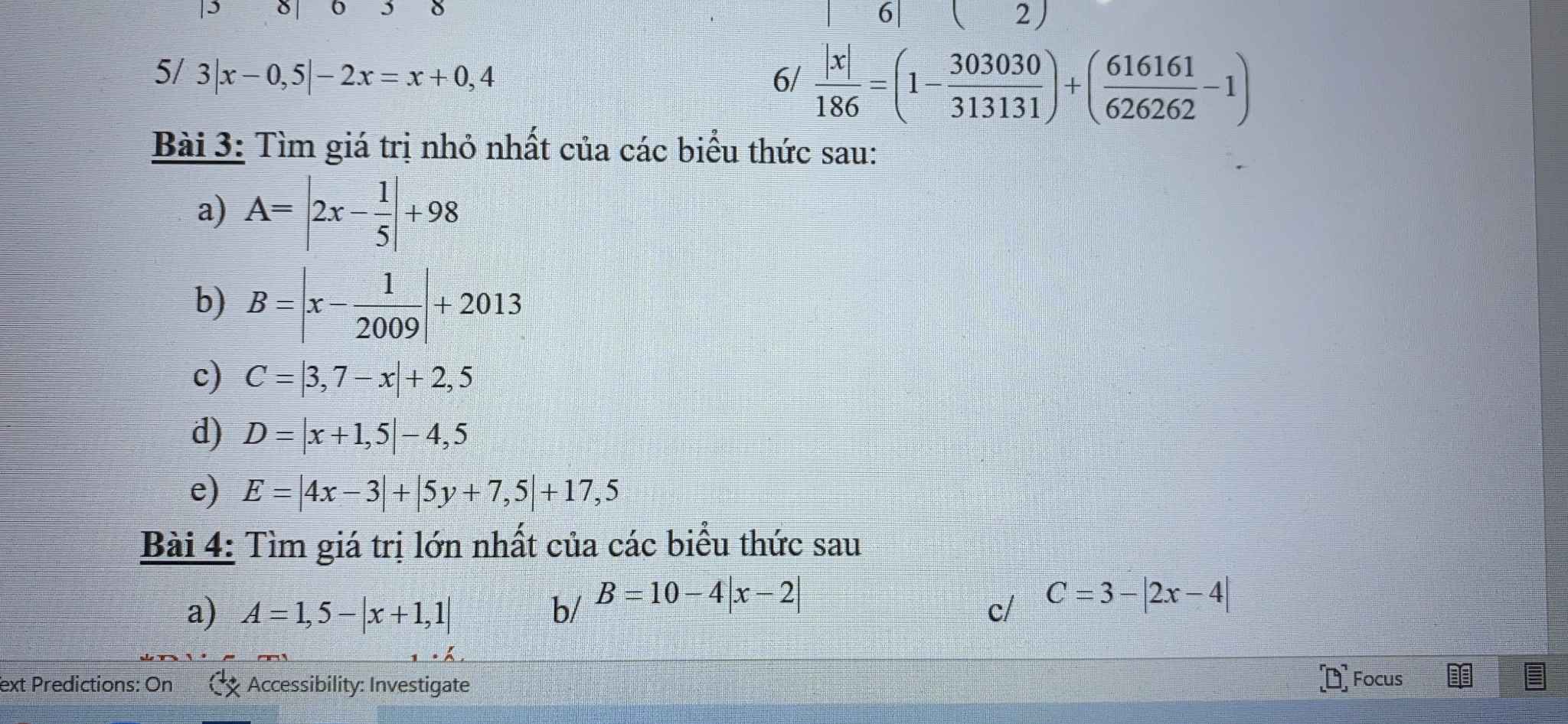
Bài 3:
a: Ta có: \(\left(2x-5\right)^2=225\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-5=15\\2x-5=-15\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=10\\x=-5\end{matrix}\right.\)
b: Ta có: \(\left|2x-3\right|=5\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=5\\2x-3=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-1\end{matrix}\right.\)