ChoΔABC vuông tại A có AB<AC và đường cao AH.C/m: BH<AH<HC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 2 2022
a: Ta có: H và D đối xứng với nhau qua AB
nên AH=AD; BH=BD
=>ΔAHD cân tại A
=>AB là tia phân giác của góc HAD(1)
Ta có: H và E đối xứng với nhau qua AC
nên AH=AE; CH=CE
=>ΔAHE cân tại A
=>AC là tia phân giác của góc HAE(2)
Từ (1) và (2) suy ra \(\widehat{EAD}=2\cdot\left(\widehat{BAH}+\widehat{CAH}\right)=2\cdot90^0=180^0\)
=>E,A,D thẳng hàng
mà AD=AE(=AH)
nên A là trung điểm của ED
b: Xét ΔDHE có
HA là đường trung tuyến
HA=DE/2
DO đó: ΔDEH vuông tại H
c: Xét ΔAHB và ΔADB có
AH=AD
HB=DB
AB chung
Do đó: ΔAHB=ΔADB
Suy ra: \(\widehat{AHB}=\widehat{ADB}=90^0\)
Xét ΔCHA và ΔCEA có
CH=CE
HA=EA
CA chung
DO đó: ΔCHA=ΔCEA
Suy ra: \(\widehat{CHA}=\widehat{CEA}=90^0\)
Xét tứ giác BDEC có BD//CE
nên BDEC là hình thang
mà \(\widehat{BDE}=90^0\)
nên BDEC là hình thang vuông
8 tháng 1 2021
a, Ta có: AM=MD (gt)
MC=MB(gt)
\(\widehat{AMC}=\widehat{BMD}\)( góc đối tạo bởi hai đường thẳng)
=> \(\Delta AMC=\Delta DMB\)(1)
b, (1) => AC=BD
c, Ta có: góc MAC= góc MBD ( ΔAMC=ΔDMB)
=> AC// BD
mà AC vuông góc AB => BD vuông góc AC
27 tháng 7 2017
https://hoc24.vn/hoi-dap/question/246500.html
đây nhé bạn
24 tháng 8 2021
a: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
\(\widehat{C}\) chung
Do đó: ΔABC\(\sim\)ΔHAC
KV
5 tháng 11 2023
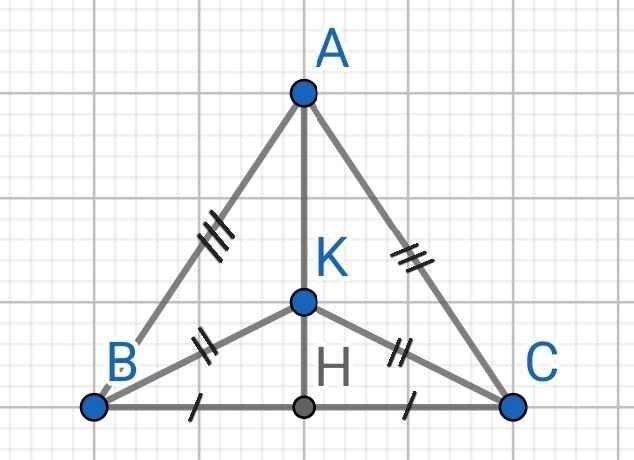
∆ABC cân tại A
⇒ H là trung điểm BC
⇒ AH là đường trung trực của ABC
⇒ AH là đường trung trực của BC
Ta có:
KB = KC (gt)
⇒ K nằm trên đường trung trực của BC
Mà AH là đường trung trực của BC
⇒ K ∈ AH
⇒ A, K, H thẳng hàng
17 tháng 3 2023
a; Xét ΔABC co AM/AB=AN/AC
nên MN//BC
=>ΔAMN đồng dạng với ΔBAC
=>\(\dfrac{S_{AMN}}{S_{ABC}}=\left(\dfrac{AM}{AB}\right)^2=\dfrac{1}{4}\)
=>\(S_{AMN}=30\left(cm^2\right)\)
b: MN/BC=AM/AB=1/2
Bạn ơi phải là AH<BH<HC nhé bạn để mink giải thích cho
Ta có AH là đừng cao => AH là đường vuông góc
Mà đường vuông góc là cạnh ngắn nhất theo định lý
=> AH < BH (1)
Ta lại có AB < AC => BH < HC ( đường xiên hình chiếu ) (2)
Từ (1) và (2) => AH<BH<HC
cảm ơn bạn