Cho tam giác ABC cân tại A,AD là đường cao,H là trực tâm ,biết góc BAC<90o,AH=14,BH=HC=30.Tính AD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AT
22 tháng 6 2021
d) Ta có: \(\angle HDA=\angle HEA=\angle DAE=90\Rightarrow HDAE\) là hình chữ nhật
\(\Rightarrow DE=AH=\sqrt{BH.HC}=\sqrt{4.9}=6\left(cm\right)\)
Ta có: \(DM\parallel EN (\bot DE)\) và \(\angle MDE=\angle DEN=90\)
\(\Rightarrow MDEN\) là hình thang vuông
Vì \(\Delta BDH\) vuông tại D có M là trung điểm BH
\(\Rightarrow MD=\dfrac{1}{2}BH=\dfrac{1}{2}.4=2\left(cm\right)\)
Vì \(\Delta HEC\) vuông tại E có M là trung điểm CH
\(\Rightarrow EN=\dfrac{1}{2}CH=\dfrac{1}{2}.9=\dfrac{9}{2}\left(cm\right)\)
\(\Rightarrow S_{DENM}=\dfrac{1}{2}.\left(DM+EN\right).DE=\dfrac{1}{2}.\left(2+\dfrac{9}{2}\right).6=\dfrac{39}{2}\left(cm^2\right)\)
21 tháng 6 2018
a) Xét \(\Delta\perp ADB\)và \(\Delta\perp AEC\)có :
\(\widehat{A}:chung\)(1)
\(AB=AC\)(vì tam giác ABC cân ) (2)
\(\widehat{ADB}=\widehat{AEC}=90^o\)(3)
Từ (1) ;(2) và (3)
\(\Rightarrow\Delta\perp ADB=\Delta\perp AEC\)( cạnh huyền - góc nhọn )
\(\Rightarrow AD=AE\)( cặp cạnh tương ứng )
b) +)
Xét \(\Delta\perp AEH\)và \(\Delta\perp ADH\)có :
\(AE=AD\) ( chứng minh ở câu a ) (1)
\(\widehat{AEH}=\widehat{ADH}=90^o\)(2)
\(AH:\)Cạnh chung (3)
Từ (1) (2)và (3)
\(\Rightarrow\Delta\perp AEH=\Delta\perp ADH\)( c-g-c)
\(\Rightarrow\widehat{EAH}=\widehat{DAH}\)( cặp góc tương ứng )
=> AH là đường phân giác của góc BAC ( đpcm )
+)
Vì \(AE=AD\)( chứng minh ở câu a )
\(\Rightarrow\Delta EAD\)Cân (1)
Mà AH là phân giác của góc BAC ( chứng minh trên ) (2)
Từ (1) và (2) => AH là đường trung trực của ED ( đpcm )
( vì trong 1 tam giác cân đường phân giác ứng với cạnh đáy đồng thời là đường trung trực -- Áp dụng định lí này nha )
c) Vì \(AB=AC\)( do tam giác ABC cân ) (1)
\(AE=AD\)( chứng minh ở câu a ) (2)
Từ (1) và (2) [ Cộng vế với vế ]
\(\Rightarrow BE=CD\)
Xét \(\Delta\perp BEH\)và \(\Delta\perp HDC\)có :
\(\widehat{BEH}=\widehat{CDH}=90^o\)(1)
\(BE=CD\)( chứng minh trên ) (2)
\(\widehat{EHB}=\widehat{HDC}\)( đối đỉnh ) (3)
Từ (1);(2) và (3)
\(\Rightarrow\Delta\perp BEH=\Delta\perp HCD\)(g.c.g)
\(\Rightarrow BE=HC\)( 2 cạnh tương ứng )
3 tháng 7 2018
a, Xét ∆ ABD và ∆ ACE có:
Góc D = góc E = 90°
AB = AC (∆ ABC cân)
Góc BAC chung
➡️∆ ABD = ∆ ACE (ch-gn)
➡️AD = AE (2 cạnh t/ư)
b, ✳️C/m AH là tia phân giác của góc BAC
Xét∆ ABC cân tại A có:
BD vuông góc với AC
CE vuông góc với AB
H là giao điểm của BD và CE
➡️H là trực tâm ∆ ABC
➡️AH vuông góc với BC
mà ∆ ABC cân tại A
➡️AH là đg cao đồng thời là đg phân giác
➡️AH là p/g góc BAC(đpcm)
✳️C/m AH là đg trung trực của ED
Xét ∆ AED cân tại A (AD = AE)
➡️AH là đg phân giác đồng thời là đg trung trực
➡️AH là đg trung trực của ED (đpcm)
c, Xét ∆ AEH và ∆ ADH có:
AE = AD (cmt)
Góc BAH = góc CAH (cmt)
AH chung
➡️∆ AEH = ∆ ADH (c.g.c)
➡️HE = HD (2 cạnh t/ư)
Xét ∆ CDH vuông tại D
➡️CH > HD
mà HE = HD (cmt)
➡️CH > HE
Còn câu d để mk nghĩ đã nhé
4 tháng 7 2018
Câu d nè bn.
d, Vì AH là đg trung trực của EF và AH vuông góc với BC
➡️ED // BC (quan hệ từ vuông góc đến song song)
Ta có: góc FED = góc DBC (2 góc có 2 cạnh tương ứng song song)
Gọi AH giao BC tại M
Xét ∆ ABC cân tại A
➡️AH là đg cao đồng thời là trung tuyến
HM là trung tuyến của BC
Xét ∆ IBC có HM là đg cao đồng thời là trung tuyến
➡️∆ IBC cân tại I
➡️Góc DBC = góc ECB
Mà góc ECB = góc DEC (2 góc so le trong)
➡️Góc DEC = góc DBC
mà góc DBC = góc FED (cmt)
➡️Góc FED = góc DEC
➡️ED là tia phân giác góc FEC
Xét ∆ FEC có: CI là phân giác góc DCE (gt)
EI là phân giác góc FEC (cmt)
CI và EI giao nhau tại I
➡️I là tâm đg tròn nội tiếp∆ FEC
➡️FI là phân giác góc CFE
mà góc CFE vuông (EF // BD, góc BDC = 90°)
➡️Góc EFI = góc CFI = 90° ÷ 2 = 45°
Vậy góc EFI = 45°
Hok tốt nhé~
3 tháng 9 2016
A B C D H E O
a/ Ta góc góc ACD chắn nửa cung AD là đường kính của (O)
=> góc ACD = 90 độ => CD vuông góc AC
Mà BH vuông góc với AC => BH // CD
b/ Tương tự ta cũng chứng minh được CH // BD
Từ câu a) có BH // CD => BHCD là hình bình hành
c/ Áp dụng công thức tính diện tích tam giác : \(S_{ABC}=\frac{1}{2}.AC^2.\frac{sinA.sinC}{sinB}=\frac{1}{2}.5^2.\frac{sin60^o.sin45^o}{sin75^o}=\frac{75-25\sqrt{3}}{4}\) (cm2)
16 tháng 3 2023
3:
\(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
HB=12^2/20=7,2cm
=>HC=20-7,2=12,8cm
\(AD=\dfrac{2\cdot12\cdot16}{12+16}\cdot cos45=\dfrac{48\sqrt{2}}{7}\)
\(HD=\sqrt{AD^2-AH^2}=\dfrac{48}{35}\left(cm\right)\)
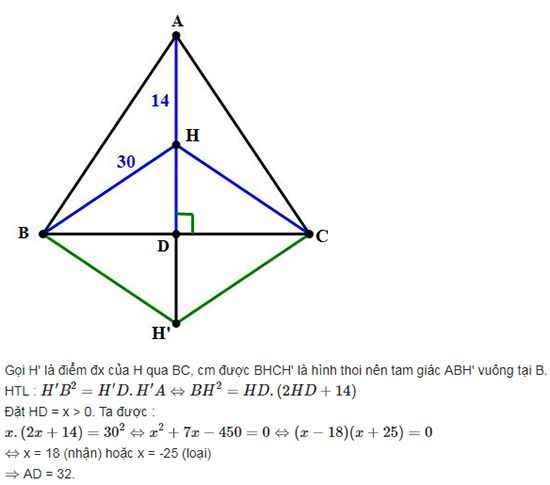
Kéo dài AD cắt đường tròn ngoại tiếp ABC tại H'.
Đặt x=HD;
Vì góc BAC nhọn và do H' đối xứng với H qua BC nên ta có: DH'=HD=x; CH'=CH=30
Áp dụng Pitago cho tg vuông ACH':
AC^2+(CH')^2=(AH')^2 -->AC^2+900=(14+2x)^2 (*)
Mặt khác CD^2= AD.DH' --> CD^2=(14+x).x (**)
trừ 2 vế (*) và (**):
AC^2+900-CD^2 =(14+2x)^2 -(14+x).x (***)
Mà AC^2-CD^2 =AD^2 =(14+x)^2;
Thế vào (***) ta được ph.tr:
(14+x)^2+900 =(14+2x)^2-(14+x)x ---> x^2+7x-450=0
phtr trên có nghiệm x= -25 (loại) và x= 18 (nhận)
AD= 14+x =14+18= 32 cm