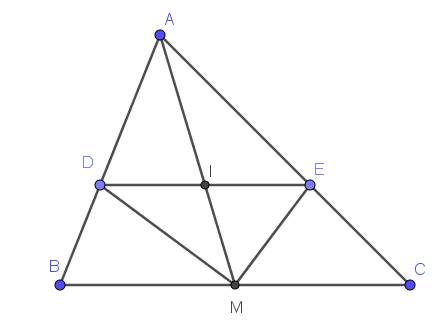
Cho tam giác ABC có đường trung tuyến AM, tia phân giác của góc AMB,AMC lần lượt cắt AB, AC tại E, D.
a, So sánh \(\dfrac{AE}{EB}\) và \(\dfrac{AD}{CD}\)
b, Gọi I là giao điểm của AM và ED. Cm I là trung điểm của ED.
c, Cho BC= 16cm, \(\dfrac{CD}{AD}=\dfrac{3}{5}\). Tính ED.
d, Gọi F và K lần lượt là giao điểm của EC với AM và DM. Cm \(EF.KC=FK.EC\).

d, Ta có : ME là tia phân giác ngoài của góc MFC => \(\dfrac{MF}{MC}=\dfrac{ÈF}{FC}\left(2\right)\)
MK là tia phân giác trong của góc MFC =>\(\dfrac{FK}{KC}=\dfrac{MF}{MC}\left(2\right)\)
Từ (1) và 2) suy ra : \(\dfrac{EF}{FC}=\dfrac{FK}{KC}\Rightarrow EF.KC=FK.EC\)
Có cần gấp lắm ko bạn @@ , nếu ko sáng mai mik làm cho :))