Không giải phương trình dùng hệ thức Viet hãy tính tổng và tích các nghiệm của mỗi pt sau:
1) mx2 – 2( m+1 ) x + m + 2 = 0 ( m khác 0)
2) ( m + 1 )x2 + mx –m +3 = 0 ( m khác –1)
3) ( 2 – ) x2 + 4x +2 + = 0
4) x2 – ( 1+ ) x + = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(x2−2x+1+2)(2x−x2−1+7)=18(x2-2x+1+2)(2x-x2-1+7)=18
⇒[(x−1)2+2][7−(x−1)2]=18(1)⇒[(x-1)2+2][7-(x-1)2]=18(1)
Đặt (x−1)2=a(x-1)2=a
(1)⇔(a+2)(7−a)=18(1)⇔(a+2)(7-a)=18
⇒−a2+5a+14=18⇒-a2+5a+14=18
⇒a2−5a+4=0⇒a2-5a+4=0
Ta có a+b+c=1−5+4=0a+b+c=1-5+4=0
⇒a1=1⇒a1=1
a2=41=4a2=41=4
Thay (x−1)2=a(x-1)2=a vào ta được
[(x−1)2=1(x−1)2=4[(x−1)2=1(x−1)2=4
⇒⎡⎢ ⎢ ⎢⎣x−1=1x−1=−1x−1=2x−1=−2⇒[x−1=1x−1=−1x−1=2x−1=−2
⇒⎡⎢ ⎢ ⎢⎣x=2x=0x=3x=−1⇒[x=2x=0x=3x=−1
Vậy nghiệm của phương trình là x={−1;0;2;3}

2.giải phương trình trên , ta được :
\(x_1=\frac{-m+\sqrt{m^2+4}}{2};x_2=\frac{-m-\sqrt{m^2+4}}{2}\)
Ta thấy x1 > x2 nên cần tìm m để x1 \(\ge\)2
Ta có : \(\frac{-m+\sqrt{m^2+4}}{2}\ge2\) \(\Leftrightarrow\sqrt{m^2+4}\ge m+4\)( 1 )
Nếu \(m\le-4\)thì ( 1 ) có VT > 0, VP < 0 nên ( 1 ) đúng
Nếu m > -4 thì ( 1 ) \(\Leftrightarrow m^2+4\ge m^2+8m+16\Leftrightarrow m\le\frac{-3}{2}\)
Ta được : \(-4< m\le\frac{-3}{2}\)
Tóm lại, giá trị phải tìm của m là \(m\le\frac{-3}{2}\)

\(a.\Leftrightarrow mx^2+2mx-x+m+2=0\)
\(\Leftrightarrow mx\left(x+2\right)+\left(m+2\right)-x=0\)
\(\Leftrightarrow\left(m+2\right)\left(mx+1\right)-x=0\)
\(\Rightarrow\left\{{}\begin{matrix}m=\left(0+x\right):\left(mx+1\right)-2\\m=[\left(0+x\right):\left(m+2\right)-1]:x\end{matrix}\right.\)

a: \(\Leftrightarrow\left(2m+4\right)^2-4m\cdot9=0\)
\(\Leftrightarrow4m^2+16m+16-36m=0\)
\(\Leftrightarrow m^2-5m+4=0\)
\(\Leftrightarrow\left(m-1\right)\left(m-4\right)=0\)
hay \(m\in\left\{1;4\right\}\)
b: \(\Leftrightarrow\left(2m-8\right)^2-4\left(m^2+m+3\right)=0\)
\(\Leftrightarrow4m^2-32m+64-4m^2-4m-12=0\)
=>-36m+52=0
=>-36m=-52
hay m=13/9
d: \(\Leftrightarrow m^2-4m\left(m+3\right)=0\)
\(\Leftrightarrow m\left(m-4m-12\right)=0\)
=>m(-3m-12)=0
=>m=0 hoặc m=-4
a) PT có nghiệm kép khi △=0
\(\Leftrightarrow\left[2\left(m+2\right)\right]^2-4.m.9=0\)
\(\Leftrightarrow4\left(m^2+4m+4\right)-36m=0\)
\(\Leftrightarrow4m^2-20m+16=0\Leftrightarrow\left[{}\begin{matrix}m=4\\m=1\end{matrix}\right.\)
Khi đó nghiệm kép của pt là \(x_1=x_2=\dfrac{-2\left(m+2\right)}{2.m}=\dfrac{-2m-4}{2m}=-1-\dfrac{2}{m}\)
+Khi m=4 thì \(x_1=x_2=-1-\dfrac{2}{4}=-\dfrac{3}{2}\)
+Khi m=1 thì \(x_1=x_2=-1-\dfrac{2}{1}=-3\)

Ta có: ∆ ’ = 2 2 – (2 - 3 )(2 + 2 ) =4 -4 - 2 2 +2 3 + 6
= 2 3 - 2 2 + 6 >0
Phương trình 2 nghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
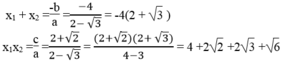

a) Để phương trình mx+2=0 là phương trình bậc nhất một ẩn thì \(m\ne0\)
b) Để phương trình \(\left(2-m\right)+2m=0\) là phương trình bậc nhất một ẩn thì \(2-m\ne0\)
hay \(m\ne2\)
c) Để phương trình \(mx^2-x+5=0\) là phương trình bậc nhất một ẩn thì m=0
d) Để phương trình \(\left(m-1\right)x^2+mx-8=0\) là phương trình bậc nhất một ẩn thì m-1=0
hay m=1

1, bạn tự giải
2,
\(\Delta'=\left(m-1\right)^2-\left(-m-3\right)=m^2-2m+1+m+3=m^2-m+4=\left(m-\dfrac{1}{2}\right)^2+\dfrac{15}{4}>0\)
Vậy pt luôn có 2 nghiệm x1 ; x2 khi \(\left(m-\dfrac{1}{2}\right)^2+\dfrac{15}{4}\ne0\left(luondung\right)\)
Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=-m-3\end{matrix}\right.\)
Ta có \(\left(x_1+x_2\right)^2-2x_1x_2=10\)
Thay vào ta được \(4\left(m-1\right)^2-2\left(-m-3\right)=10\)
\(\Leftrightarrow4m^2-8m+4+2m+6=10\Leftrightarrow4m^2-6m=0\)
\(\Leftrightarrow m\left(4m-6\right)=0\Leftrightarrow m=0;m=\dfrac{3}{2}\)
mô ra rựa? cấy ni k có trong đề cương dé!!!!
hc đi, ngồi bấm lung tung là c qua c lia cho chiếc dép vô mặt là coi chừng dé!!!
dạ c e xl nha
e xl nha e qua nhà c e bơ cho vài phát vỡ mồm dé!!!
e qua nhà c e bơ cho vài phát vỡ mồm dé!!! k có trong đề cương r sao, vc e hs là của e dé!!! lo mà rep ib đi cher cẩn thận hềy
k có trong đề cương r sao, vc e hs là của e dé!!! lo mà rep ib đi cher cẩn thận hềy