(VD) Tìm x...
Đọc tiếp
(VD) Tìm x biết
b, format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22math1da40657c9fece7e48d30af42d3%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%226.5%22%20y%3D%2226%22%3E%26%23x2212%3B%3C%2Ftext%3E%3Cline%20stroke%3D%22%23000000%22%20stroke-linecap%3D%22square%22%20stroke-width%3D%221%22%20x1%3D%2215.5%22%20x2%3D%2227.5%22%20y1%3D%2220.5%22%20y2%3D%2220.5%22%2F%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2221.5%22%20y%3D%2215%22%3E9%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2221.5%22%20y%3D%2237%22%3E4%3C%2Ftext%3E%3Ctext%20font-family%3D%22math1da40657c9fece7e48d30af42d3%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2237.5%22%20y%3D%2226%22%3E%26%23x2212%3B%3C%2Ftext%3E%3Cline%20stroke%3D%22%23000000%22%20stroke-linecap%3D%22square%22%20stroke-width%3D%221%22%20x1%3D%2247.5%22%20x2%3D%2259.5%22%20y1%3D%2220.5%22%20y2%3D%2220.5%22%2F%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2253.5%22%20y%3D%2215%22%3E5%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2253.5%22%20y%3D%2237%22%3E8%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2264.5%22%20y%3D%2226%22%3E%3A%3C%2Ftext%3E%3C%2Fsvg%3E)
xformat('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22math17f39f8317fbdb1988ef4c628eb%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2212.5%22%20y%3D%2226%22%3E%3D%3C%2Ftext%3E%3Cline%20stroke%3D%22%23000000%22%20stroke-linecap%3D%22square%22%20stroke-width%3D%221%22%20x1%3D%2227.5%22%20x2%3D%2239.5%22%20y1%3D%2220.5%22%20y2%3D%2220.5%22%2F%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2233.5%22%20y%3D%2215%22%3E3%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2233.5%22%20y%3D%2237%22%3E7%3C%2Ftext%3E%3C%2Fsvg%3E)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 11 2021
Áp dụng tc dtsbn:
\(3x=7y\Rightarrow\dfrac{x}{7}=\dfrac{y}{3}=\dfrac{x-y}{7-3}=\dfrac{-16}{4}=-4\\ \Rightarrow\left\{{}\begin{matrix}x=-28\\y=-12\end{matrix}\right.\)
LM
3
30 tháng 10 2021
b) \(\Leftrightarrow3x^3+12x-2x^2-8=0\\ \Leftrightarrow\left(3x^3-2x^2\right)+\left(12x-8\right)=0\\ \Leftrightarrow x^2\left(3x-2\right)+4\left(3x-2\right)=0\\ \Leftrightarrow\left(x^2+4\right)\left(3x-2\right)=0\)
Vì \(x^2+4>0\Rightarrow3x-2=0\Rightarrow x=\dfrac{2}{3}\)
c) \(x^2+5x=0\\ \Leftrightarrow x\left(x+5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
d) \(\Leftrightarrow x^3-27+x\left(4-x^2\right)=36\\ \Leftrightarrow x^3+4x-x^3=63\\ \Leftrightarrow4x=63\\ \Leftrightarrow x=\dfrac{63}{4}\)
HL
30 tháng 10 2021
b) 3x(x\(^3\) +12x-2x\(^2\)-8=0
3x(x\(^2\)+4)-2(x\(^2\)+4)=0
(x\(^2\)+4)(3x-2)=0
\(\Leftrightarrow\left[{}\begin{matrix}X^2+4=0\\3X-2=0\end{matrix}\right.\) <=> \(\left[{}\begin{matrix}x\in Z\\X=\dfrac{2}{3}\end{matrix}\right.\)
a) x\(^2\)+5x=0
x(x+5)=0
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+5=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
c)(x-3)(x\(^2\)+3x+9)+x(x+2)(2-x)=36
x\(^3\)-27+x(x+2)(2-x)=36
4x-27=36
4x=36+27
4x=63
x=\(\dfrac{63}{4}\)
13 tháng 3 2021
B-(\(3x^6-4xy^5+\dfrac{1}{3}xy^2\))=
B= \(\left(7x^6-\dfrac{1}{2}xy^5-xy^2-\dfrac{1}{3}\right)+\left(3x^6-4xy^5+\dfrac{1}{3}xy^2-\dfrac{3}{2}\right)\)
B= \(7x^6-\dfrac{1}{2}xy^5-xy^2-\dfrac{1}{3}+3x^6-4xy^5+\dfrac{1}{3}xy^2-\dfrac{3}{2}\)
B= \(7x^6+3x^6-\dfrac{1}{2}xy^5-4xy^5-xy^2+\dfrac{1}{3}xy^2-\dfrac{1}{3}+\dfrac{2}{3}\)
B= \(10x^6-\dfrac{9}{2}xy^5-\dfrac{2}{3}xy^2+\dfrac{1}{3}\)
VV
25 tháng 10 2021
\(1\)/
\(a\)) \(=\left(\dfrac{7}{5}-\dfrac{8}{7}\right)+\dfrac{17}{5}:0,6\)
\(=\dfrac{9}{35}+\dfrac{17}{3}\)
\(=\dfrac{622}{105}\)
\(b\)) \(=\dfrac{11}{6}+\dfrac{-14}{15}\)
\(=\dfrac{9}{10}\)
\(c\)/ \(=\dfrac{7}{4}-\dfrac{2}{3}\)
\(=\dfrac{13}{12}\)
NC
2
HG
15 tháng 6 2019
Bài đó không cần dùng bảng xét dấu cũng được mà bạn
M=\(\left(x+3\right)\left(x+4\right)\)
\(\text{M dương }\Leftrightarrow\text{M}\ge0\Leftrightarrow\left(x+3\right)\left(x+4\right)\ge0\)
\(\text{TH1}:\)
\(\hept{\begin{cases}x+3\ge0\\x+4>0\end{cases}\Leftrightarrow\hept{\begin{cases}x\ge-3\\x>-4\end{cases}}}\Rightarrow x\ge3\)
\(\text{TH2}:\)
\(\hept{\begin{cases}x+3\le0\\x+4< 0\end{cases}\Leftrightarrow\hept{\begin{cases}x\le-3\\x< -4\end{cases}}}\Rightarrow x\le3\)
\(\text{Vậy với }x\ge3\text{ hoặc }x\le3\text{ thì M dương }\)
15 tháng 6 2019
Bài này không cần dùng bảng xét dấu đâu bạn. Bạn lập luận như sau:
M dương khi: (x+3) và (x+4) cùng dấu
TH1: (x+3) > 0 => x > -3
(x+4) > 0 => x > -4
=> x > -3
TH2: (x+3) < 0 => x < -3
(x+4) < 0 => x < -4
=> x < -4
Vậy x > -3 hoặc x < -4
\(\Leftrightarrow\orbr{\begin{cases}\hept{\begin{cases}x+3>0\:\Leftrightarrow\:x>-3\\x+4>0\:\Leftrightarrow\:x>-4\end{cases}}\\\hept{\begin{cases}x+3< 0\:\Leftrightarrow\:x< -3\\x+4< 0\:\Leftrightarrow\:x< -4\end{cases}}\end{cases}}\Rightarrow\:\)
N
3
12 tháng 5 2017
muốn tìm một số x khi biết gtri của nó:( mk ns theo vd của bn nha)
- nếu mẫu số chưa phải là 1 số dương thì bn phải lm cho mẫu số là 1 số dương
- sau đó quy đồng mẫu số cho cả 2 vế
=> thực hiện tiếp phép tính như thường thôi
:)
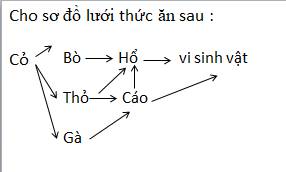
IKIHJHJJJN .?
\(-\frac{9}{4}-\frac{5}{8}\div x=\frac{3}{7}\)
\(\frac{5}{8}\div x=-\frac{9}{4}-\frac{3}{7}\)
\(\frac{5}{8}\div x=-\frac{75}{28}\)
\(x=\frac{5}{8}\div\left(-\frac{75}{28}\right)\)
\(x=-\frac{7}{30}\)