Cho tam giác ABC cân tại A, AH,BK là đường cao của tam giác.Tính BC biết AH=15,6 và BK=12
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

cho tam giac ABC cân tại A , AH vuông góc với BC , BK vuông góc với AC , AH=15,6 ; BK=12 . Tính BC ?


a: AH*BC=BK*AC
=>BC/AC=BK/AH=6/5
=>BH/AC=3/5
=>CH/AC=3/5
=>CH/3=AC/5=k
=>CH=3k; AC=5k
AH^2+HC^2=AC^2
=>16k^2=32^2=1024
=>k^2=64
=>k=8
=>CH=24cm; AC=40cm
=>BC=48cm; AB=40cm
b: Xét ΔCKB vuông tại K và ΔCHA vuông tại H có
góc C chung
=>ΔCKB đồng dạng với ΔCHA
=>CK/CH=CB/CA
=>CK*CA=CH*CB=1/2BC^2
=>2*CK*CA=BC^2

a: Xét ΔCKB vuông tại K và ΔCHA vuông tại H có
góc C chung
=>ΔCKB đồng dạng với ΔCHA
=>CK/CH=CB/CA
=>CA*CK=CH*CB
b: BH=CH=10/2=5cm
AH=căn 13^2-5^2=12cm
BK*AC=AH*BC
=>BK*13=12*10=120
=>BK=120/13(cm)

Tham khảo
a) Ta có: AB = AC (gt); AI = IB = 1/2AB (Cmt); AK = KC = 1/2 AC (gt)
AB = AI + IB
AC = AK + KC
=> AI = AK
Ta lại có: t/giác ABC cân tại A; AH là đường cao
=> AH là đường p/giác (t/c của t/giác cân)
=> góc BAH = góc CAH
hay góc IAG = góc KAG
b) Xét t/giác IAG và t/giác KAG
có IA = AK (cmt)
góc IAG = góc KAG (cmt)
AG : chung
=> t/giác IAG = t/giác KAG (c.g.c)
c) Ta có: AI = AK (cm câu b)
=> t/giác AIK cân tại A
=> góc AIK = góc AKI = (180 độ - góc A)/2 (1)
Ta lại có: t/giác ABC cân tại A
=> góc B = góc C = (180 độ - góc A)/2 (2)
Từ (1) và (2) suy ra góc AIK = góc B
Mà góc AIK và góc B ở vị trí đồng vị
=> IK // BC
refer
a) Ta có: AB = AC (gt); AI = IB = 1/2AB (Cmt); AK = KC = 1/2 AC (gt)
AB = AI + IB
AC = AK + KC
=> AI = AK
Ta lại có: t/giác ABC cân tại A; AH là đường cao
=> AH là đường p/giác (t/c của t/giác cân)
=> góc BAH = góc CAH
hay góc IAG = góc KAG
b) Xét t/giác IAG và t/giác KAG
có IA = AK (cmt)
góc IAG = góc KAG (cmt)
AG : chung
=> t/giác IAG = t/giác KAG (c.g.c)
c) Ta có: AI = AK (cm câu b)
=> t/giác AIK cân tại A
=> góc AIK = góc AKI = (180 độ - góc A)/2 (1)
Ta lại có: t/giác ABC cân tại A
=> góc B = góc C = (180 độ - góc A)/2 (2)
Từ (1) và (2) suy ra góc AIK = góc B
Mà góc AIK và góc B ở vị trí đồng vị
=> IK // BC

???, bạn ơi, hình như có 2 điểm M, : " AM cắt BC,BK lần lượt tại M và N " ?


A B C H K
dựa vào Pi-ta-go, tính được 18 cm và tam giác ABC cân tại A nên H sẽ là trung điểm của CB => HC=15cm
dễ dàng chứng minh \(\Delta AHC\infty\Delta BKC\left(g-g\right)\)
=>\(\frac{HC}{KC}=\frac{AC}{BC}\Rightarrow\frac{AC}{30}=\frac{15}{18}=\frac{5}{6}\Rightarrow AC=25\)
và đến đây dựa vào Pi-ta-go tính được AH=20
^_^

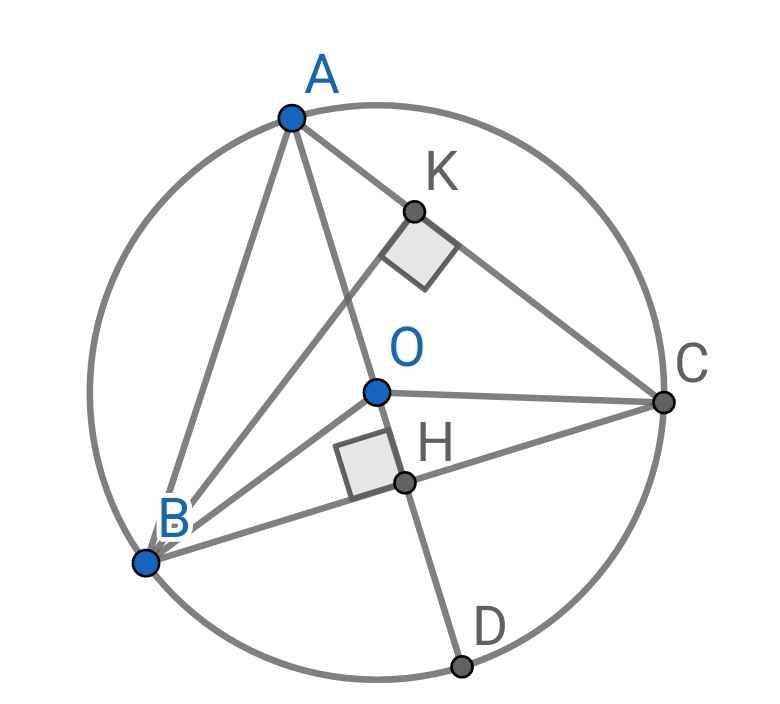 a) Ta có:
a) Ta có:
OB = OC (bán kính)
⇒ O nằm trên đường trung trực của BC (1)
Do ∆ABC cân tại A (gt)
AH là đường cao (gt)
⇒ AH cũng là đường trung trực của ∆ABC
⇒ AH là đường trung trực của BC (2)
Từ (1) và (2) suy ra O ∈ AH
⇒ O ∈ AD
Vậy AD là đường kính của (O)
b) Sửa đề: Tính độ dài các đường cao AH, BK của ∆ABC
Do AH là đường trung trực của BC (cmt)
⇒ H là trung điểm của BC
⇒ CH = BC : 2
= 12 : 2
= 6 (cm)
∆AHC vuông tại H
⇒ AC² = AH² + CH² (Pytago)
⇒ AH² = AC² - CH²
= 10² - 6²
= 64
⇒ AH = 8 (cm)
⇒ sinACH = AH/AC
= 4/5
⇒ ACH ≈ 53⁰
⇒ BCK ≈ 53⁰
∆BCK vuông tại K
⇒ sinBCK = BK/BC
⇒ BK = BC.sinBCK
= 10.sin53⁰
≈ 8 (cm)
