Từ 1 điểm M ở bên ngoài đường tròn (O;R), vẽ tiếp tuyến MA (A là tiếp điểm) và cát tuyến MBC sao cho \(\widehat{BAC}< 90^o\) Tia phân giác AD của \(\widehat{BAC}\) (\(D\in BC\)) cắt (O) tại E, H là hình chiếu của A trên MO
a) Chứng minh: \(BE=CE\)
b) Chứng minh: \(\Delta\) MAD cân
c) Chứng minh: \(MD^2=MB.MC\)
d) Chứng minh: Tứ giác BHOC nội tiếp
e) Chứng minh: \(AB.AC=AD^2+DB.DC\)
f) Gọi K là giao điểm của MO và (O)....
Đọc tiếp
Từ 1 điểm M ở bên ngoài đường tròn (O;R), vẽ tiếp tuyến MA (A là tiếp điểm) và cát tuyến MBC sao cho \(\widehat{BAC}< 90^o\) Tia phân giác AD của \(\widehat{BAC}\) (\(D\in BC\)) cắt (O) tại E, H là hình chiếu của A trên MO
a) Chứng minh: \(BE=CE\)
b) Chứng minh: \(\Delta\) MAD cân
c) Chứng minh: \(MD^2=MB.MC\)
d) Chứng minh: Tứ giác BHOC nội tiếp
e) Chứng minh: \(AB.AC=AD^2+DB.DC\)
f) Gọi K là giao điểm của MO và (O). Chứng minh \(BM.HK=BH.MK\)
Ai giúp mình câu F với, còn mỗi câu ấy thôi
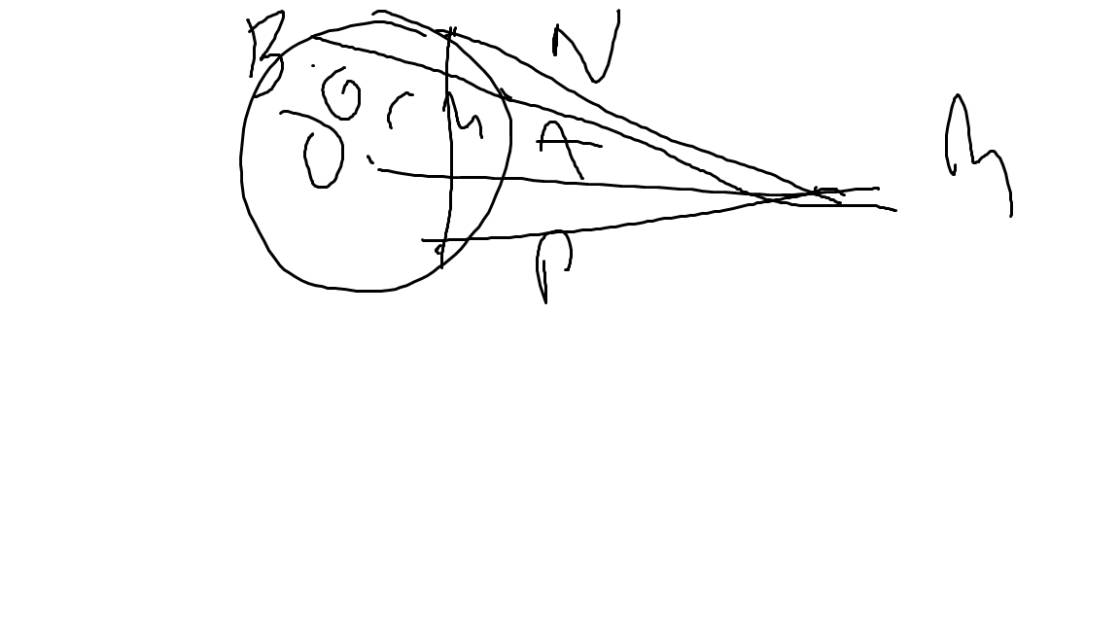
Câu f)
Theo phần d đã chứng minh được $BHOC$ nội tiếp
\(\Rightarrow \widehat{MHB}=\widehat{MCO}\)
Xét tam giác $MHB$ và $MCO$ có:
\(\left\{\begin{matrix} \widehat{MHB}=\widehat{MCO}\\ \text{Chung góc M}\end{matrix}\right.\Rightarrow \triangle MHB\sim \triangle MCO(g.g)\)
\(\Rightarrow \frac{MB}{HB}=\frac{MO}{CO}(1)\)
Giờ ta sẽ chứng minh \(\frac{MO}{CO}=\frac{KM}{KH}\)
\(\Leftrightarrow MO.KH=KM.CO\)
\(\Leftrightarrow MO.KH=CO(MO+OK)\)
\(\Leftrightarrow CO.OK=MO(KH-CO)=MO(KH-KO)\)
\(\Leftrightarrow CO^2=MO.OH\)
\(\Leftrightarrow OA^2=OH.OM\) (đúng theo hệ thức lượng trong tam giác vuông MAO)
Do đó \(\frac{MO}{CO}=\frac{KM}{KH}\). Kết hợp với (1) suy ra \(\frac{KM}{KH}=\frac{BM}{BH}\Rightarrow MK.BH=BM.HK\)
Bạn ơi, mình học là cái dấu hiệu góc ngoài tại 1 đỉnh bằng góc trong tại định đó chỉ được dùng để chứng minh chứ không được dùng làm định lí
Giờ sao ???