ΔBCD cân tại B, kẻ 2 đường cao CH và DK cắt nhau ở K.
a. Chứng minh CH = DK
b. Chứng minh ΔCED cân
c. Chứng minh KH // CD
d. Biết BE cắt CD ở I. Chứng minh BI là đường cao cũng là trung tuyết của ΔBCD
e. Chứng minh BI < CD/2 + BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CH
Cô Hoàng Huyền
Admin
VIP
1 tháng 2 2018
Câu hỏi của Bảo Châu Trần - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo lời giải tại đây nhé.
LD
18 tháng 4 2018
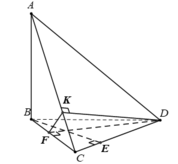
Bài 5:
Cho ABC vuông tại A, kẻ phân giác BM ( M AC), trên cạnh BC
lấy điểm E sao cho BE = AB
a) Chứng minh 2 tam giác BAM BEM .
b) Gọi F là giao điểm của đường thẳng ME và đường thẳng AB.
Chứng minh: FM = MC.
c) Chứng minh: AM < MC
d) Chứng minh AE // FC.
CH
Cô Hoàng Huyền
Admin
VIP
1 tháng 2 2018
a) Ta thấy ngay \(\Delta ABE=\Delta ACD\) (Hai cạnh góc vuông)
b) Do \(\Delta ABE=\Delta ACD\Rightarrow\widehat{ABE}=\widehat{ACD}\)
mà \(\widehat{ABE}=\widehat{MAC}\) (Cùng phụ với góc BEA)
\(\Rightarrow\widehat{MAC}=\widehat{MCA}\) hay tam giác MAC cân tại M.
c) Xét tam giác vuông ADC: \(\widehat{MCA}=\widehat{MAC}\Rightarrow\widehat{MDA}=\widehat{MAD}\Rightarrow MD=MA\)
Vậy thì DM = MA = MC hay M là trung điểm DC.
Xét tam giácAIC có M là trung điểm DC, MK // DI nên MK là đường trung bình tam giác DIC.
Suy ra K là trung điểm IC.
d) Xét tam giác DIC có IM và DK là hai trung tuyến nên G là trọng tâm tam giác.
Gọi N là giao điểm của CG với DE thì DN = NI.
Áp dụng định lý Talet ta có:
\(\frac{MF}{DN}=\frac{CF}{CN}=\frac{FK}{NI}\)
Mà DN = NI nên MF = FK.
6 tháng 2 2022
a: Xét ΔABD vuông tại B và ΔACD vuông tại C có
AD chung
AB=AC
Do đó: ΔABD=ΔACD
nên DB=DC
b: BE⊥AC
DC⊥AC
Do đó: BE//DC
c: \(\widehat{EBC}=\widehat{DCB}\)
mà \(\widehat{DCB}=\widehat{DBC}\)
nên \(\widehat{EBC}=\widehat{DBC}\)
hay BC là tia phân giác của góc EBD
d: Ta có: AB=AC
nên A nằm trên đường trung trực của BC(1)
Ta có: DB=DC
nên D nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra AD vuông góc BC
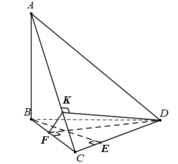
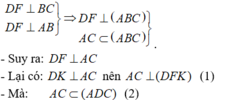
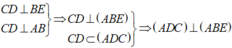
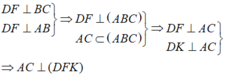
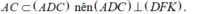
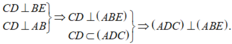
a: Xét ΔBCH vuông tại H và ΔBDK vuông tại K có
BC=BD
góc B chung
Do đó: ΔBCH=ΔBDK
Suy ra: CH=DK
b: Xét ΔECD có góc ECD=góc EDC
nên ΔECD cân tại E
c: Xét ΔBCD có BK/BC=BH/BD
nên KH//CD