Question

[Lê Vũ Yến Nhi]

Bài 3 : (2,0 điểm).

Cho biểu thức 

a) Rút gọn biểu thức A.

b) Tìm x để 

Bài 4 : (3,5 điểm).

Cho tam giác ABC vuông tại A, đường cao AH. Biết BC = 8cm, BH = 2cm.

a) Tính độ dài các đoạn thẳng AB, AC, AH.

b) Trên cạnh AC lấy điểm K (K A, K C), gọi D là hình chiếu của A trên BK. Chứng minh rằng: BD.BK = BH.BC

c) Chứng minh rằng:

Answer 1

[Nguyễn Huy Tú]

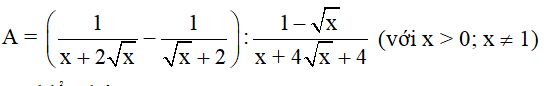
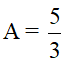
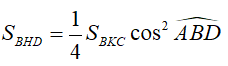
Bài 4 : 

a, Xét tam giác ABC vuông tại A, đường cao AH 

* Áp dụng hệ thức : \(AB^2=BH.BC=16\Rightarrow AB=4\)cm 

Theo định lí Ptago : \(AC=\sqrt{BC^2-AB^2}=\sqrt{64-16}=4\sqrt{3}\)cm 

* Áp dụng hệ thức : \(AH.BC=AB.AC\Rightarrow AH=\frac{AB.AC}{BC}=\frac{16\sqrt{3}}{8}=2\sqrt{3}\)cm 

b, Xét tam giác ABK vuông tại A, đường cao AD 

\(AB^2=BD.BK\)( hệ thức lượng ) (1) 

Xét tam giác ABC vuông tại A, đường cao AH

\(AB^2=BH.BC\)( hệ thức lượng ) (2) 

Từ (1) ; (2) => \(BD.BK=BH.BC\)(3) 

c, Xét tam giác BHD và tam giác BKC 

^B _ chung 

(3) => \(BD.BK=BH.BC\Rightarrow\frac{BD}{BC}=\frac{BH}{BK}\)

Vậy tam giác BHD ~ tam giác BKC ( c.g.c )

=> \(\frac{S_{BHD}}{S_{BKC}}=\left(\frac{BD}{BC}\right)^2\)(4) 

Ta có : cosABD = \(\frac{DB}{AB}\)

=> cos²ABD = \(\left(\frac{DB}{AB}\right)^2\)=> cos²ABD = \(\frac{DB^2}{AB^2}=\frac{DB^2}{16}\)

=> \(\frac{1}{4}cos^2\widehat{ABD}=\frac{DB^2}{64}=\frac{DB^2}{8^2}=\frac{DB^2}{BC^2}=\left(\frac{DB}{BC}\right)^2\)

\(\Rightarrow\frac{1}{4}cos^2\widehat{ABD}=\frac{S_{BHD}}{S_{BKC}}\)theo (4) 

=> \(S_{BHD}=S_{BKC}.\frac{1}{4}cos^2\widehat{ABD}\)

Answer 2

[Nguyễn Huy Tú]

Bài 3 : 

a, Với \(x>0;x\ne1\)

\(A=\left(\frac{1}{x+2\sqrt{x}}-\frac{1}{\sqrt{x}+2}\right):\frac{1-\sqrt{x}}{x+4\sqrt{x}+4}\)

\(=\left(\frac{1-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)}\right):\frac{1-\sqrt{x}}{\left(\sqrt{x}+2\right)^2}=\frac{\sqrt{x}+2}{\sqrt{x}}\)

b, Ta có : \(A=\frac{5}{3}\Rightarrow\frac{\sqrt{x}+2}{\sqrt{x}}=\frac{5}{3}\Rightarrow3\sqrt{x}+6=5\sqrt{x}\Leftrightarrow6=2\sqrt{x}\Leftrightarrow x=9\)