Tìm GTNN của A = \(\dfrac{32}{x^2+2x+4}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
30 tháng 7 2021
1.
$x(x+2)(x+4)(x+6)+8$
$=x(x+6)(x+2)(x+4)+8=(x^2+6x)(x^2+6x+8)+8$
$=a(a+8)+8$ (đặt $x^2+6x=a$)
$=a^2+8a+8=(a+4)^2-8=(x^2+6x+4)^2-8\geq -8$
Vậy $A_{\min}=-8$ khi $x^2+6x+4=0\Leftrightarrow x=-3\pm \sqrt{5}$
AH
Akai Haruma
Giáo viên
30 tháng 7 2021
2.
$B=5+(1-x)(x+2)(x+3)(x+6)=5-(x-1)(x+6)(x+2)(x+3)$
$=5-(x^2+5x-6)(x^2+5x+6)$
$=5-[(x^2+5x)^2-6^2]$
$=41-(x^2+5x)^2\leq 41$
Vậy $B_{\max}=41$. Giá trị này đạt tại $x^2+5x=0\Leftrightarrow x=0$ hoặc $x=-5$
30 tháng 8 2023
\(B=-\left(\dfrac{4}{9}x-\dfrac{2}{15}\right)^6+3\)
vì \(B=-\left(\dfrac{4}{9}x-\dfrac{2}{15}\right)^6\le0,\forall x\inℝ\)
\(\Rightarrow B=-\left(\dfrac{4}{9}x-\dfrac{2}{15}\right)^6+3\le3\)
Dấu "=" xảy ra khi và chỉ khi
\(\dfrac{4}{9}x-\dfrac{2}{15}=0\Rightarrow\dfrac{4}{9}x=\dfrac{2}{15}\Rightarrow x=\dfrac{9}{15}\)
Vậy \(GTLN\left(B\right)=3\left(tạix=\dfrac{9}{15}\right)\)
30 tháng 8 2023
\(A=\left(2x+\dfrac{1}{3}\right)^4-1\)
vì \(\left(2x+\dfrac{1}{3}\right)^4\ge0,\forall x\inℝ\)
\(\Rightarrow A=\left(2x+\dfrac{1}{3}\right)^4-1\ge-1\)
Dấu "=" xảy ra khi và chỉ khi
\(2x+\dfrac{1}{3}=0\Rightarrow2x=-\dfrac{1}{3}\Rightarrow x=-\dfrac{1}{6}\)
\(\Rightarrow GTNN\left(A\right)=-1\left(tạix=-\dfrac{1}{6}\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 4 2021
a.
\(A=\dfrac{2013}{x^2}-\dfrac{2}{x}+1=2013\left(\dfrac{1}{x}-\dfrac{1}{2013}\right)^2+\dfrac{2012}{2013}\ge\dfrac{2012}{2013}\)
Dấu "=" xảy ra khi \(x=2013\)
b.
\(B=\dfrac{4x^2+2-4x^2+4x-1}{4x^2+2}=1-\dfrac{\left(2x-1\right)^2}{4x^2+2}\le1\)
\(B_{max}=1\) khi \(x=\dfrac{1}{2}\)
\(B=\dfrac{-2x^2-1+2x^2+4x+2}{4x^2+2}=-\dfrac{1}{2}+\dfrac{\left(x+1\right)^2}{2x^2+1}\ge-\dfrac{1}{2}\)
\(B_{max}=-\dfrac{1}{2}\) khi \(x=-1\)
1 tháng 1 2021
Ta có: \(\left(x-1\right)^2+\left(x+y\right)^2\le9\Rightarrow x+y\le3\).
Áp dụng bất đẳng thức AM - GM ta có:
\(\dfrac{2}{x}+2x\ge2\sqrt{\dfrac{2}{x}.2x}=4;\dfrac{4}{y}+y\ge2\sqrt{\dfrac{4}{y}.y}=4\).
Do đó \(\dfrac{2}{x}\ge4-2x;\dfrac{4}{y}\ge4-y\)
\(\Rightarrow P\ge8-4\left(x+y\right)\ge-4\). (do \(x+y\le3\)).
Vậy...
Đẳng thức xảy ra khi và chỉ khi x = 1; y = 2.
HA
1
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 3 2021
\(A=1-\dfrac{2}{x}+\dfrac{1975}{x^2}=1975\left(\dfrac{1}{x}-\dfrac{1}{1975}\right)^2+\dfrac{1974}{1975}\ge\dfrac{1974}{1975}\)
\(A_{min}=\dfrac{1974}{1975}\) khi \(x=1975\)
TG
1
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 1 2024
Đặt \(x-1=t\Rightarrow x=t+1\)
\(A=\dfrac{2\left(t+1\right)^2-6\left(t+1\right)+5}{t^2}=\dfrac{2t^2-2t+1}{t^2}=\dfrac{1}{t^2}-\dfrac{2}{t}+2=\left(\dfrac{1}{t}-1\right)^2+1\ge1\)
\(A_{min}=1\) khi \(t=1\Rightarrow x=2\)
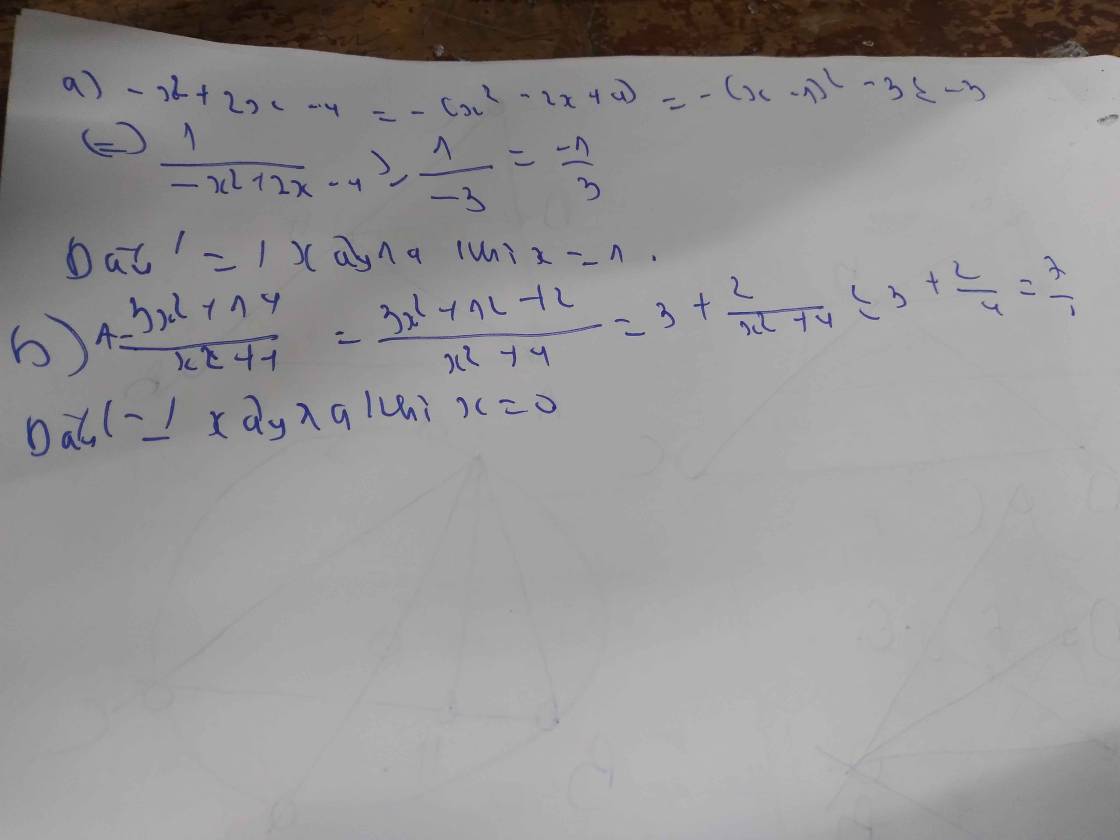
\(A=\dfrac{32}{x^2+2x+4}=\dfrac{32}{x^2+2x+1+3}=\dfrac{32}{\left(x^2+2x+1\right)+3}\)
= \(\dfrac{32}{\left(x+1\right)^2+3}\)
do (x+1)2 ≥ 0 ∀x
=> (x+1)2+3 ≥ 3
=> \(\dfrac{32}{\left(x+1\right)^2+3}\le\dfrac{32}{3}\)
=> A ≤ \(\dfrac{32}{3}\)
max A= \(\dfrac{32}{3}\) dấu "=" xảy ra khi
x+1=0
=> x=-1
vậy max A= \(\dfrac{32}{3}\) khi x=-1