Giúp em bài 81 được ko ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 3.
a. Ta có: \(CK=BK\left(gt\right)\Rightarrow OK\perp BC\)
Ta có: \(\widehat{OIC}=90^o\)
\(\widehat{OKC}=90^o\)
\(\Rightarrow\widehat{OIC}+\widehat{OKC}=90^o+90^o=180^o\)
`=>` Tứ giác CIOK nội tiếp đường tròn
b. Xét \(\Delta AID\) và \(\Delta CIB\), có:
\(\widehat{AID}=\widehat{CIB}=90^o\left(gt\right)\)
\(\widehat{ADI}=\widehat{CBI}\) ( cùng chắn \(\stackrel\frown{AC}\) )
Vậy \(\Delta AID\sim\Delta CIB\) ( g.g)
\(\Rightarrow\dfrac{IA}{IC}=\dfrac{ID}{IB}\)
\(\Leftrightarrow IC.ID=IA.IB\)
c. Kẻ \(DM\perp AC\)
Ta có: \(\widehat{ACB}=90^o\) ( góc nt chắn nửa đtròn )
`->` Tứ giác DMCK là hình chữ nhật
\(\rightarrow DK\perp BC\)
Mà \(OK\perp BC\)
\(\Rightarrow\) 3 điểm D,O,K thẳng hàng

a: Khi m=3 thì (1): x^2-6x+4=0
=>x^2-6x+9-5=0
=>(x-3)^2=5
=>\(x=3\pm\sqrt{5}\)

#include <bits/stdc++.h>
using namespace std;
long long n,i,t,x,y,ln;
int main()
{
cin>>n;
ln=LLONG_MIN;
for (i=1; i<=n; i++)
if (n%i==0)
{
if (ln<=i+n/i)
{
ln=i+n/i;
x=i;
y=n/i;
}
}
cout<<x<<" "<<y;
}


Số học sinh đạt điểm khá là:
400:100x45=180(bạn)
Đáp số: 180 bạn
@Teoyewmay

a, Vì D,M là trung điểm AB,AC nên DM là đtb tg ABC
Do đó \(DM=\dfrac{1}{2}BC=\dfrac{7}{2}\left(cm\right)\) và DM//BC

10: =>1/2x=3/4 và x+y=2
=>x=3/4*2=3/2 và y=1/2
11:=>4x+5y=3 và 4x-12y=20
=>17y=-17 và x-3y=5
=>y=-1 và x=3y+5=-3+5=2
12: =>7x-2y=1 và 6x+2y=12
=>13x=13 và 3x+y=6
=>x=1 và y=3
13:=>2/x=1 và 1/x-1/y=1/5
=>x=2 và 1/y=1/2-1/5=3/10
=>y=10/3 và x=2
14: =>12/x-16/y=8 và 12/x-15/y=9
=>-1/y=-1 và 4/x-5/y=3
=>y=1 và 4/x=3+5=8
=>x=1/2 và y=1



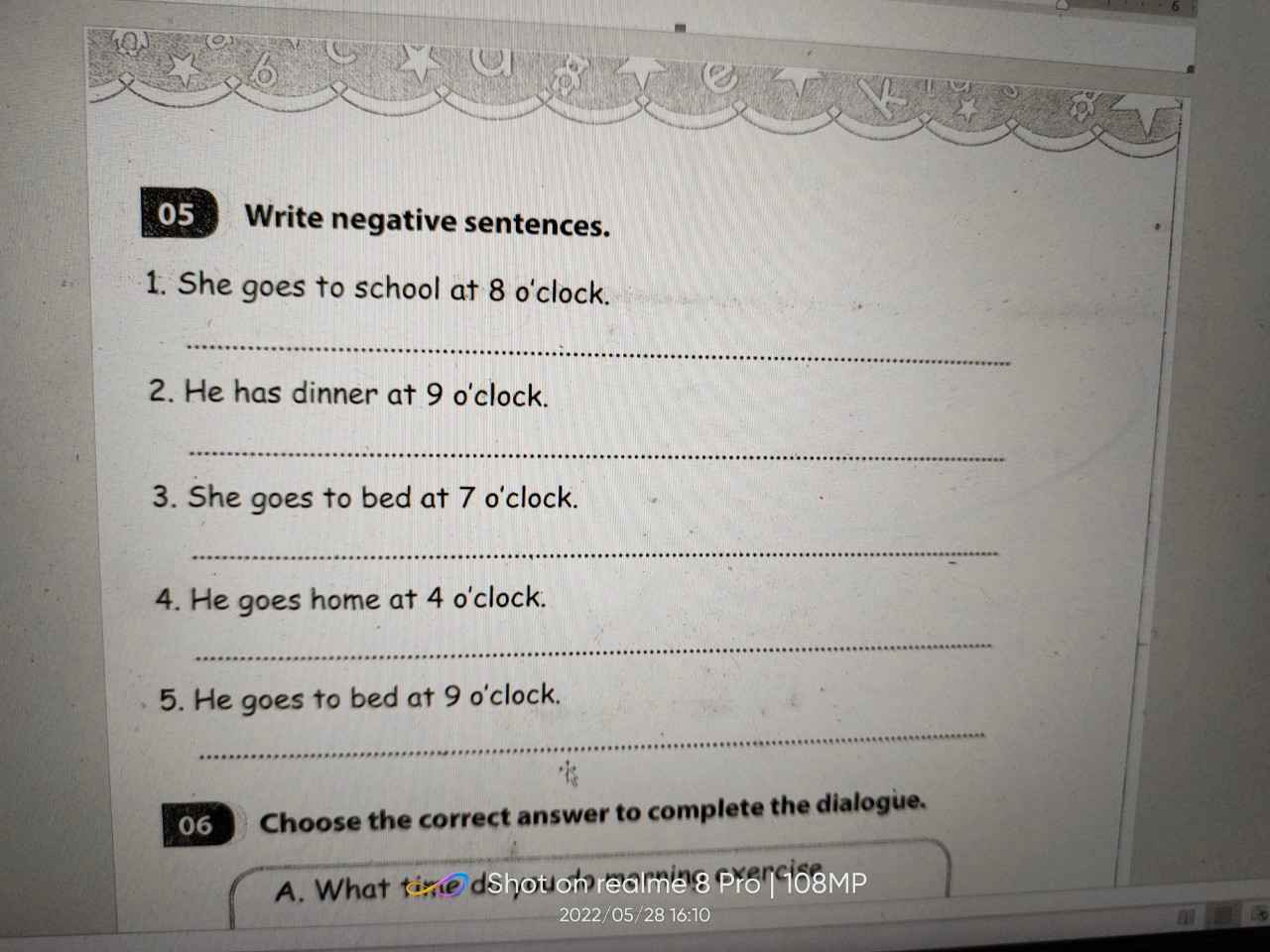
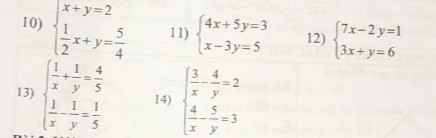
81a.
$A=x(x+2)(x+3)(x+5)+9$
$=x(x+5)(x+2)(x+3)+9=(x^2+5x)(x^2+5x+6)+9$
$=(x^2+5x)^2+6(x^2+5x)+9$
$=(x^2+5x+3)^2$
81b.
$B=(x+2)(x+4)(x+6)(x+8)+16=(x+2)(x+8)(x+4)(x+6)+16$
$=(x^2+10x+16)(x^2+10x+24)+16$
$=a(a+8)+16$ (đặt $x^2+10x+16=a$)
$=a^2+8a+16=(a+4)^2=(x^2+10x+16+4)^2$
$=(x^2+10x+20)^2$
81c.
$C=(x^2+x)^2+9x^2+9x+14=(x^2+x)^2+9(x^2+x)+14$
$=a^2+9a+14$ (đặt $x^2+x=a$)
$=(a^2+7a)+(2a+14)=a(a+7)+2(a+7)$
$=(a+2)(a+7)=(x^2+x+2)(x^2+x+7)$
81d.
$D=x^2+2xy+y^2+2x+2y-15$
$=(x^2+2xy+y^2)+(2x+2y)-15=(x+y)^2+2(x+y)-15$
$=a^2+2a-15$ (đặt $x+y=a$)
$=(a^2-3a)+(5a-15)=a(a-3)+5(a-3)=(a-3)(a+5)$
$=(x+y-3)(x+y+5)$
81e.
$E=x^2-2xy+y^2+2x-2y-3=(x^2-2xy+y^2)+(2x-2y)-3$
$=(x-y)^2+2(x-y)-3=a^2+2a-3$ (đặt $x-y=a$)
$=(a^2-a)+(3a-3)=a(a-1)+3(a-1)=(a+3)(a-1)$
$=(x-y+3)(x-y-1)$
81g.
$G=(x^2+x)^2+5y(x^2+x)+6y^2$
$=(x^2+x)^2+2y(x^2+x)+3y(x^2+x)+6y^2$
$=(x^2+x)(x^2+x+2y)+3y(x^2+x+2y)$
$=(x^2+x+2y)(x^2+x+3y)$
81h.
$H=(x^2-x+1)(x^2+3x+1)+4x^2$
$=(a-x)(a+3x)+4x^2$ (đặt $x^2+1=a$)
$=a^2+2ax+x^2=(a+x)^2=(x^2+1+x)^2$