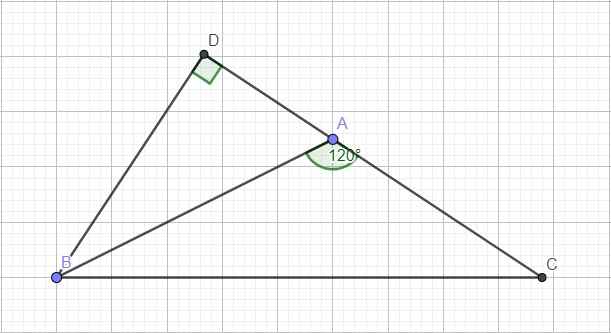
Cho ΔABC có góc A bằng 2 lần góc B. gọi BC= a, AC= b, AB= c. Chứng minh hệ thức a2 = b2 + bc
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Kẻ đường cao BD ứng với AC. Do góc A tù \(\Rightarrow\) D nằm ngoài đoạn thẳng AC hay \(CD=AD+AC\) và \(\widehat{DAB}=180^0-120^0=60^0\)
Áp dụng định lý Pitago:
\(AB^2=BD^2+AD^2\) \(\Rightarrow BD^2=AB^2-AD^2\)
Trong tam giác vuông ABD:
\(cos\widehat{BAD}=\dfrac{AD}{AB}\Rightarrow\dfrac{AD}{AB}=cos60^0=\dfrac{1}{2}\Rightarrow AD=\dfrac{1}{2}AB\)
\(\Rightarrow BD^2=AB^2-\left(\dfrac{1}{2}AB^2\right)=\dfrac{3}{4}AB^2\)
Pitago tam giác BCD:
\(BC^2=BD^2+CD^2=\dfrac{3}{4}AB^2+\left(AD+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\left(\dfrac{1}{2}AB+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\dfrac{1}{4}AB^2+AB.AC+AC^2\)
\(=AB^2+AB.AC+AC^2\)
Hay \(a^2=b^2+c^2+bc\)


Gọi G là giao điểm của AM và BN.
Theo công thức tính độ dài đường trung tuyến: \(AM^2=\dfrac{2b^2+2c^2-a^2}{4}\);
\(BN^2=\dfrac{2c^2+2a^2-b^2}{4}\).
Từ đó \(AG^2=\dfrac{4}{9}AM^2=\dfrac{2b^2+2c^2-a^2}{9}\); \(BG^2=\dfrac{4}{9}BN^2=\dfrac{2c^2+2a^2-b^2}{9}\).
Do đó \(AG^2+BG^2=\dfrac{a^2+b^2+4c^2}{9}=\dfrac{9c^2}{9}=c^2=AB^2\).
Theo định lý Pythagoras đảo thì tam giác AGB vuông tại G.
Vậy góc giữa 2 trung tuyến AM và BN là 90o.

a,Ta có : ABC^+BAC^+BCA^=180* ( đl tổng 3 góc )
=> 90*+BAC^+30*=180*
=>BAC^=180*-120*=60*
Do AM là tia p/g của BAC^
=> BAM^=MAN^=60*/2=30*
Xét tam giác vuông ABM và tam giác vuông ANM
AM cạnh chung
BAM^=MAN^
=>tam giác ABM = tam giác ANM ( ch-gn )
=>AB=AN (2 cạnh tương ứng)
b,Xét tam giác vuông IBM và tam giác vuông CNM
BMI^=NMC^ ( đối đỉnh )
BM = NM ( cm câu a )
=> tam giác IBM = tam giác CNM ( cgv-gn )
c, Ta có : BMI^ + MBI^ + BIM ^ = 180*
=>BMI^ + 90* + 30* = 180*
=> BMI^=180*-120*=60*
Do BMI^=CMN^
=>BMI^=CMN^=60*
Lại có IMN^=180* ( góc bẹt )
Mà : IMC^+CMN^=180*
=>IMC^=180*-60*=120*
Mặt khác : IM=MC (cm câu b)
=> tam giác IMC cân tại M
=>MIC^=MCI^
dễ thấy : IMC^+MIC^+MCI^=180*
=>MIC^+MCi^=180*-120*=60*
do :MIC^=MCI^
=>MIC^=MCI^=60*/2=30*
Ta có :+)AIC^=BIM^+CIM^=30*+30*=60*
+)ACI^=NCM^+MCI^=30*+30*=60*
+)IAC^=60*
=>tam giác IAC là tam giác đều

a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Xét ΔBAE vuông tại A và ΔBDE vuông tại D có
BE chung
\(\widehat{ABE}=\widehat{DBE}\)
Do đó: ΔBAE=ΔBDE
Suy ra: BA=BD; EA=ED
c: Xét ΔAEK vuông tại A và ΔDEC vuông tại D có
EA=ED
\(\widehat{AEK}=\widehat{DEC}\)
Do đó:ΔAEK=ΔDEC
Suy ra: EK=EC

Bài 1: Ta có hình vẽ sau:
B A C M E
a)Xét ΔABM và ΔECM có:
BM = CM (gt)
\(\widehat{AMB}=\widehat{EMC}\) (đỗi đỉnh)
MA = ME (gt)
=> ΔABM = ΔACM (c.g.c) (đpcm)
b) Vì ΔABM = ΔECM (ý a)
=> \(\widehat{MAB}=\widehat{MEC}\) (2 góc tương ứng)
mà 2 góc này lại ở vị trí so le trong nên
=> AB // CE (đpcm)
Bài 5: Ta có hình vẽ sau:
O A B D C x y E
a) Vì OA = OB (gt) và AC = BD (gt)
=> OC = OD
Xét ΔOAD và ΔOBC có:
OA = OB (gt)
\(\widehat{O}\) : Chung
OC = OD (cm trên)
=> ΔOAD = ΔOBC (c.g.c)
=> AD = BC (2 cạnh tương ứng)(đpcm)
b) Vì ΔOAD = ΔOBC(ý a)
=> \(\widehat{OBC}=\widehat{OAD}\) và \(\widehat{ODA}=\widehat{OCB}\)
(những cặp góc tương ứng)
Xét ΔEAC và ΔEBD có:
\(\widehat{OBC}=\widehat{OAD}\) (cm trên)
AC = BD (gt)
\(\widehat{ODA}=\widehat{OCB}\) (cm trên)
=> ΔEAC = ΔEBD (g.c.g) (đpcm)
c) Vì ΔEAC = ΔEBD (ý b)
=> EA = EB (2 cạnh tương ứng)
Xét ΔOAE và ΔOBE có:
OA = OB (gt)
\(\widehat{OBC}=\widehat{OAD}\) (đã cm)
EA = EB (cm trên)
=> ΔOAE = ΔOBE (c.g.c)
=> \(\widehat{AOE}=\widehat{BOE}\) (2 góc tương ứng)
=> OE là phân giác của \(\widehat{xOy}\)