Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tgiac ABD và EBD có:
+ AB = BE
+ BD chung
+ góc ABD = EBD
=> Tgiac ABD = EBD (c-g-c)
=> đpcm
b) Tgiac ABD = EBD (cmt) => AD = DE (hai cạnh t/ứng)
Xét tgiac ADE có AD = DE => Tgiac ADE cân tại D
=> đpcm
c) AH \(\perp\)BC, DE\(\perp\)BC => AH\(//\)DE
=> góc HAE = AED (2 góc SLT do AH\(//\)DE)
Mà tgiac ADE cân tại D (cmt) => góc AED = DAE
=> góc HAE = DAE
=> AE là tia pgiac góc HAC (đpcm)
d) Xét tgiac ADK và EDC có:
+ góc DAK = DEC = 90o
+ góc ADK = EDC (2 góc đối đỉnh)
+ AD = DE (do tgiac ABD = EBD)
=> Tgiac ADK = EDC (g-c-g)
=> AK = EC và KD = DC (2 cạnh t/ứng)
=> Tgiac KDC cân tại K => Góc DCK = (180o- góc KDC) /2
Tgiac AED cân tại D => góc EAD = (180o- góc ADE) /2
Mà góc ADE = KDC (2 góc đối đỉnh) => góc DCK = EAD
Mà 2 góc này SLT => AE \(//\)KC
=> đpcm

A B C H D K
(Ký hiệu thêm điểm E cho mình nhé)
a/ Theo đề bài ta có:
\(AB^2+AC^2=BC^2\)
\(5^2+12^2=13^2\)
\(25+144=169\)(Luôn đúng)
=> Định lý Pytago
Mà định lý này chỉ sử dụng trong tam giác vuông => tam giác ABC vuông tại A
(Nếu đề có cho độ dài cạnh mà kêu cminh tam giác hay góc vuông thì cứ dùng pytago đảo. Mà lâu chưa làm không biết trình bày logic chưa, có gì thông cảm nhé)
Cạnh huyền của tam giác vuông là cạnh dài nhất: đó là cạnh BC
b/ Xét tam giác ABE và tam giác DEB có:
\(\hept{\begin{cases}\widehat{ABE}=\widehat{CBE}\left(gt\right)\\BE:chung\\\widehat{BAE}=\widehat{BDE}=90^0\left(gt\right)\end{cases}}\)
\(\Rightarrow\Delta ABE=\Delta DBE\left(g.c.g\right)\)
\(\Rightarrow AB=BD\)
Mà: AB = 5 cm => BD = 5 cm
c/ Cái này làm chả biết đúng không.
Gọi H là giao điểm của BE và KC
Xét tam giác ABC có 2 đường cao AC;KD cắt nhau tại E => E là trực tâm tam giác ABC
=> BE là đường cao thứ 3
=> BE vuông góc KC tại H
Xét tam giác BKC có BH vừa là đường cao vừa là pgiác => tam giác BKC cân tại B => \(BK=BC\)(1)
* Xét tam giác BKH vuông tại H có BK là cạnh huyền => \(KH< BK\)(2)
* Xét tam giác BHC vuông tại H có BC là cạnh huyền => \(HC< BC\)(3)
Từ (1);(2);(3) \(\Rightarrow KH+HC< BK+BC\)
\(\Leftrightarrow KC< 2BC\left(đpcm\right)\)

4:
a: Xet ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
b: Xet ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF
c: AE=AF
ME=MF
=>AM là trung trực của EF
mà K nằm trên trung trực của EF
nên A,M,K thẳng hàng

a) Xét ΔABD và ΔEBD có
BA=BE(gt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔABD=ΔEBD(c-g-c)
Suy ra: \(\widehat{BAD}=\widehat{BED}\)(hai góc tương ứng)
mà \(\widehat{BAD}=90^0\)(ΔABC vuông tại A)
nên \(\widehat{BED}=90^0\)
hay DE\(\perp\)BC(Đpcm)
b) Ta có: ΔBAD=ΔBED(cmt)
nên AD=ED(hai cạnh tương ứng)
Xét ΔADK vuông tại A và ΔEDC vuông tại E có
DA=DE(cmt)
\(\widehat{ADK}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔADK=ΔEDC(cạnh góc vuông-góc nhọn kề)
Suy ra: AK=EC(hai cạnh tương ứng)
c) Ta có: BA+AK=BK(A nằm giữa B và K)
BE+EC=BC(E nằm giữa B và C)
mà BA=BE(cmt)
và AK=EC(cmt)
nên BK=BC
Ta có: ΔADK=ΔEDC(cmt)
nên DK=DC(hai cạnh tương ứng)
Ta có: M là trung điểm của CK(cmt)
nên MK=MC
Ta có: BK=BC(cmt)
nên B nằm trên đường trung trực của KC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: DK=DC(cmt)
nên D nằm trên đường trung trực của KC(Tính chất đường trung trực của một đoạn thẳng)(2)
Ta có: CM=KM(cmt)
nên M nằm trên đường trung trực của KC(Tính chất đường trung trực của một đoạn thẳng)(3)
Từ (1), (2) và (3) suy ra B,D,M thẳng hàng(đpcm)

a) Xét tam giác BHA và BHE có:
BD chung
ˆABD^=ˆEBD^(vì BD là phân giác ˆBB^)
ˆBHA^=ˆBHE^(vì AH vuông góc với Bd tại H)
⇒Tam giác BHA=tam giac BHE(c.g.v-g.n.k)
b) Xét Tam giác BDA và tam giác BDE có
BD chung
BA=BE( vì tam giac BHA = tam giac BHE( chứng minh phần a))
ABD=EBD( vì BD là phân giác củaˆBB^)
⇒⇒Tam giác BDA = Tam giác BDE(c.g.c)
⇒⇒ˆBEA^=ˆA^= 90o(2 canh tương ứng và ˆA^= 90o)
ED vuông góc với B tại E
c, AD = DE
DE < CD do tam giác CDE vuông tại E
=> AD < DC
d, DA= DE do tam giác ABD = tam giác EBD (Câu b)
=> tam giác DAE cân tại D (đn)
=> ^DAE = ^DEA (tc) (1)
có : AK _|_ BC (gt) ; DE _|_ BC (câu b)
=> DE // AK
=> ^DEA = ^EAK (slt) và (1)
=> ^DAE = ^EAK mà AE nằm giữa AD và AK
=> AE là phân giác của ^CAK (đpcm)
a) Vì EH ⊥ BC ( gt )
=> ΔBHE vuông tại H
Xét tam giác vuông BAE và tam giác vuông BHE có :
BE chung
∠B1 = ∠B2 ( BE là tia phân giác của ∠BAC )
=> ΔBAE = ΔBHE ( cạnh huyền - góc nhọn )
b) Gọi I là giao điểm của AH và BE
Xét ΔABI và ΔHBI có :
BA = BH (ΔBAE = ΔBHE (cmt)
∠B1 = ∠B2 ( BE là tia phân giác của ∠BAC )
BI chung
=> ΔABI = ΔHBI ( c.g.c )
=> ∠AIB = ∠AIH ( 2 góc tương ứng )
Mà ∠AIB + ∠AIH = 1800 ( 2 góc kề bù )
=> ∠AIB = ∠AIH = 900
=> BI ⊥ AH (1)
Ta có: IA = IH ( ΔABI = ΔHBI ( cmt )
Mà I nằm giữa hai điểm A và H (2)
=> I là trung điểm của AH ( 3)
Từ (1) (2) (3) => BI là trung trực của AH
Hay BE là trung trực của AH
c) Xét ΔKAE và ΔCHE có:
∠KAE = ∠CHE ( = 900 )
AE = HE ( ΔBAE = ΔBHE (cmt)
∠AEK = ∠HEC ( 2 góc đối đỉnh )
=> ΔKAE = ΔCHE ( g.c.g )
=> EK = EC ( 2 cạnh tương ứng )

a.Ta có:
⎧⎪⎨⎪⎩BA=BEˆABD=ˆDBEchungBD→ΔABD=ΔEBD(c.g.c){BA=BEABD^=DBE^chungBD→ΔABD=ΔEBD(c.g.c)
b.Từ câu a→ˆBED=ˆBAD=90o→BED^=BAD^=90o
→DE⊥BC→DE⊥BC
c.Ta có:
ˆBKD+ˆADK=ˆACB+ˆDEC=90oBKD^+ADK^=ACB^+DEC^=90o
→ˆBKD=ˆACB→BKD^=ACB^
→ΔBDK=ΔBDC(g.c.g)→ΔBDK=ΔBDC(g.c.g)
→BK=BC→BK=BC


a) Xét tam giác BAD và tam giác BED ta có
AB=AD(gt)
góc B1= góc B2 (tia phân giác)
BD chung
tam giác BAD = tam giác BED (c.g.c)
Suy ra: góc A = góc E ( 2 góc tương ứng )
b) Ta có : góc H =E ( =90 độ)
suy ra : AH//DE ( vì AH và DE cùng vuông với BC)
Còn câu c để mình nghĩ lốt nha

2:
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
b: Xét ΔDAK vuông tại A và ΔDEC vuông tại E có
DA=DE
góc ADK=góc EDC
=>ΔDAK=ΔDEC
=>DK=DC
=>ΔDKC cân tại D


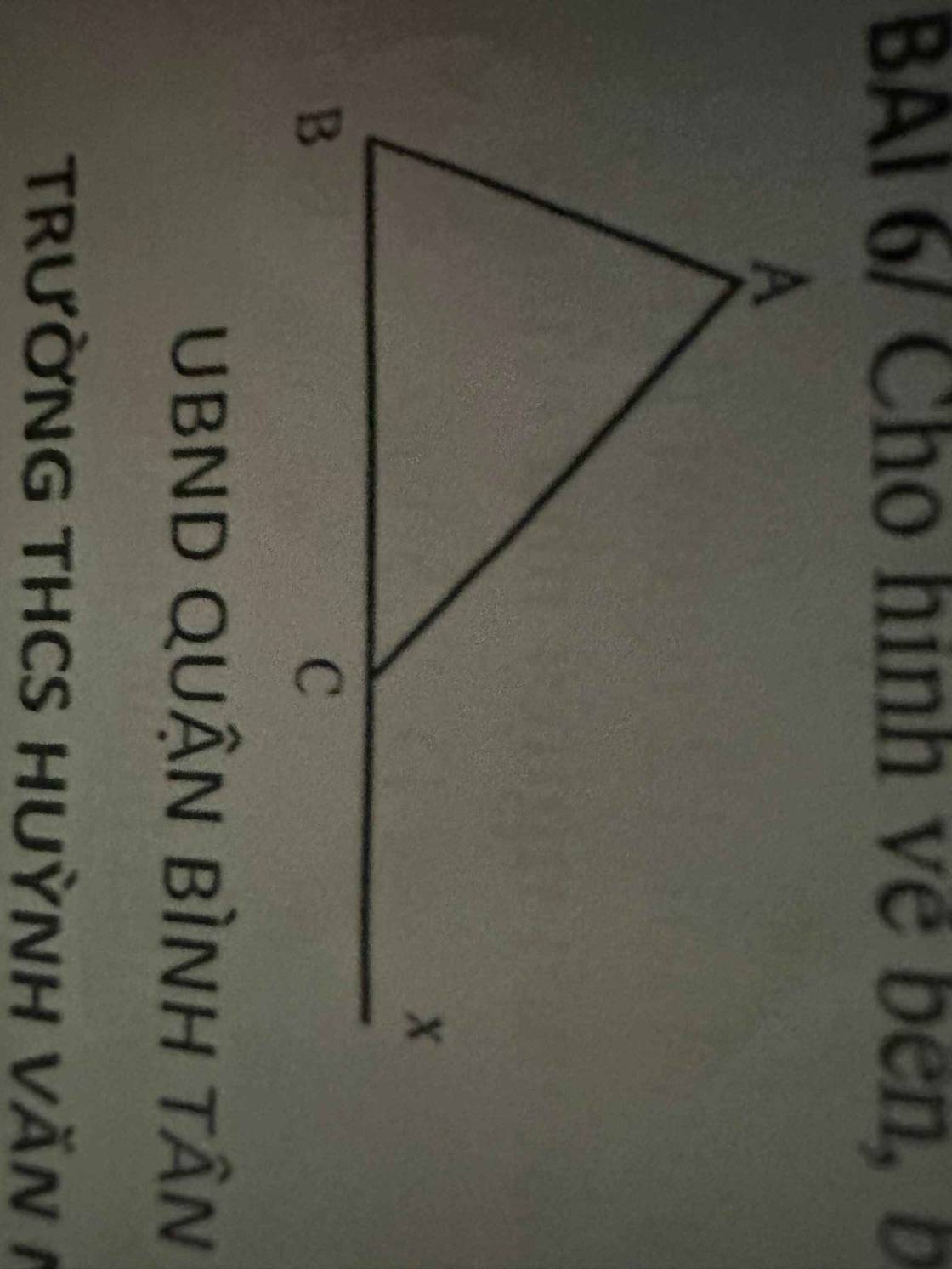
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Xét ΔBAE vuông tại A và ΔBDE vuông tại D có
BE chung
\(\widehat{ABE}=\widehat{DBE}\)
Do đó: ΔBAE=ΔBDE
Suy ra: BA=BD; EA=ED
c: Xét ΔAEK vuông tại A và ΔDEC vuông tại D có
EA=ED
\(\widehat{AEK}=\widehat{DEC}\)
Do đó:ΔAEK=ΔDEC
Suy ra: EK=EC