Biết rằng hai đa thức P(x) và Q(x) đều có nghiệm. Có thể kết luận rằng đa thức P(x) + Q(x) phải nghiệm hay không? Em có thể lập luận để chứng tỏ câu trả lời của em là đúng hay sai ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 4 2019
TA CÓ
\(p\left(\frac{1}{2}\right)=4\cdot\left(\frac{1}{2}\right)^2-4\cdot\frac{1}{2}+1=4\cdot\frac{1}{4}-2+1\)
\(=1-2+1=0\)
vậy ......
TA CÓ
\(x^2\ge0\Rightarrow4x^2\ge0\Rightarrow4x^2+1\ge1\)hay\(4x^2+1>0\)
vậy..............
4 tháng 4 2019
Thay \(x=\frac{1}{2}\)vào P (x) ta có:
\(P\left(\frac{1}{2}\right)=4.\left(\frac{1}{2}\right)^2-4.\frac{1}{2}+1\)
\(P\left(\frac{1}{2}\right)=4.\frac{1}{4}-2+1\)
\(P\left(\frac{1}{2}\right)=1-2+1\)
\(P\left(\frac{1}{2}\right)=0\)
Vậy \(x=\frac{1}{2}\) là nghiệm của P(x)
24 tháng 8 2021
a: Ta có: \(P=x^5-3x^2+7x^4-9x^3+x^2-\dfrac{1}{4}x\)
\(=x^5+7x^4-9x^3-2x^2-\dfrac{1}{4}x\)
Ta có: \(Q=5x^4-x^5+x^2-2x^3+3x^2-\dfrac{1}{4}\)
\(=-x^5+5x^4-2x^3+4x^2-\dfrac{1}{4}\)
29 tháng 6 2022
KHông thể kết luận được rằng M(x)+N(x) luôn có nghiệm
VD như \(M\left(x\right)=x^2+3x+2\) có 2 nghiệm là x=-1 và x=-2
\(N\left(x\right)=5x+15\) có 1 nghiệm là x=-3
Nhưng \(M\left(x\right)+N\left(x\right)=x^2+8x+17=\left(x+4\right)^2+1>0\)
=>M(x)+N(x) vô nghiệm
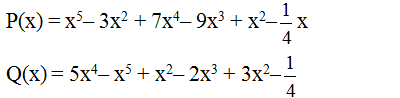
Không thể kết luận P(x)+Q(x) có nghiệm được
Vd như \(P\left(x\right)=x^2+3x+2\) có hai nghiệm là -1 và -2
\(Q\left(x\right)=5x+15\) có nghiệm là -3
nhưng \(P\left(x\right)+Q\left(x\right)=x^2+8x+17=\left(x+4\right)^2+1>0\forall x\)
=>P(x)+Q(x) vô nghiệm