Coi khoảng cách tối thiểu an toàn của hai xe ô tô đang chạy trên đường là bằng "một nửa vận tốc (theo đơn vị km/h) tính bằng mét". Thí dụ khi xe chạy với vận tốc 60km/h thì khoảng cách tối thiểu an toàn là 30m. Hai ô tô giống nhau chuyển động trên đường thẳng với cùng vận tốc, đồng thời khoảng cách giữa chúng bằng khoảng cách an toàn tối thiểu. Cho rằng ô tô thứ nhất bắt đầu giảm vận tốc và sau một thời gian nào đó thì dừng lại. Người lái xe ô tô thứ hai bắt đầu phát hiện ô tô thứ nhất giảm vận tốc sau thời gian t nào đó và cũng bắt đầu giảm vận tốc cho tới khi dừng lại như xe trước. Nhưng người lái xe thứ hai không phát hiện nhanh thì ô tô sẽ va chạm. Hãy tìm thời gian phản ứng t lớn nhất của người lái xe thứ hai theo công thức "một nửa vận tốc (theo đơn vị km/h) tính bằng mét" để các ô tô không va chạm.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
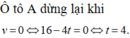
Quãng đường ô tô A đi được kể từ thời điểm bắt đầu hãm phanh đến lúc dừng lại là:
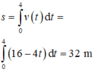
Do đó ô tô A phải hãm phanh khi cách ô tô B một khoảng tối thiểu là 32+1=33m

Đáp án A
Phương pháp
S = ∫ t 1 t 2 v t d t
Cách giải
v = 0 ⇒ t = 4
Quãng đường ô tô A đi được từ khi bắt đầu hãm phanh đến khi dừng hẳn
là S = ∫ 0 4 16 − 4 t d t = 32
Khi dừng lại ô tô A phải cách ô tô B tối thiểu 1m nên để có 2 ô tô A và B đạt khoảng cách an toàn thì ô tô A phải hãm phanh cách ô tô B một khoảng ít nhất là 33m.

Vận tốc trung bình của ô tô chạy trên quãng đường đó là:
(60+40):2=50(km)
Đáp số:50km/h.

Ta có: v = 90 km/h = 25 m/s; v0 = 0; s = 70 m; m = 2,5 tấn = 2500 kg.
Gia tốc tối thiểu của xe là:
\(a = \frac{{{v^2} - v_0^2}}{{2.s}} = \frac{{{{25}^2}}}{{2.70}} = \frac{{125}}{{28}}(m/{s^2})\)
=> Lực tối thiểu để xe bán tải dừng lại an toàn: \(F = m.a = 2500.\frac{{125}}{{28}} \approx 11160,71(N)\)

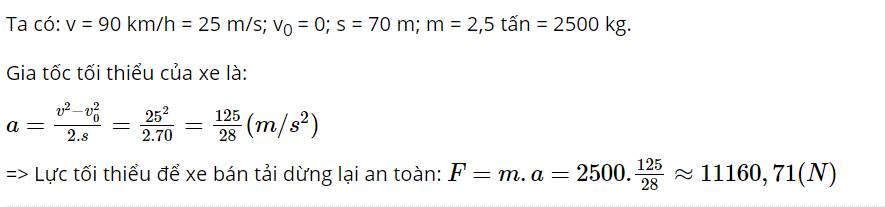
Bạn cần mk giải ko