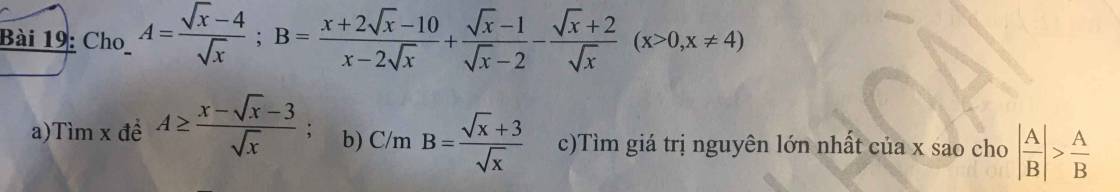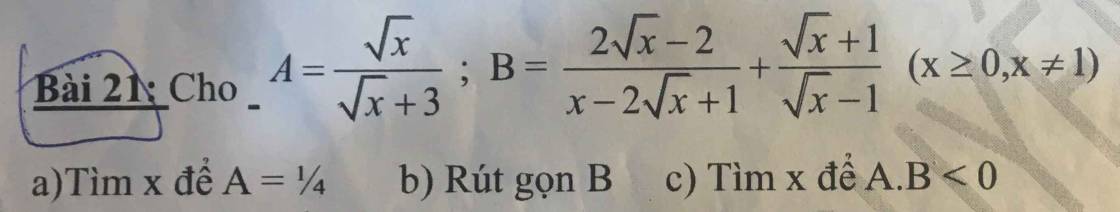Giúp mình mấy bài này được không ạ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


like playing soccer, don't you
goes to school late, doesn't he
can swim very well, can't you
is going to the party, isn't she
was published in Germany in 1550, wasn't it
are sold all over the world, aren't they
have been built this year, haven't they
was given a book, wasn't he
were bought by Mrs Brown yesterday, weren't they
is used everyday, isn't it

a: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
=>\(\widehat{AMB}=90^0\)
b: Xét ΔOMC vuông tại M có MH là đường cao
nên \(HC\cdot HO=HM^2\left(1\right)\)
Xét ΔMAB vuông tại M có MH là đường cao
nên \(HA\cdot HB=HM^2\left(2\right)\)
Từ (1) và (2) suy ra \(HC\cdot HO=HA\cdot HB\)
c: Xét tứ giác AMBQ có
O là trung điểm của AB và MQ
Do đó: AMBQ là hình bình hành
Hình bình hành AMBQ có AB=MQ
nên AMBQ là hình bình hành

unpollute
deforestation
environmental
pollution
conservationists
prevention
extremely
environmentalist
protection
seriously
poisonous

f, \(3sin^2x-cosx+2cos2x-3=0\)
\(\Leftrightarrow3-3cos^2x-cosx+2\left(2cos^2x-1\right)-3=0\)
\(\Leftrightarrow cos^2x-cosx-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=-1\\cosx=2\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow x=\pi+k2\pi\)
h, \(cos^2x+cos^22x+cos^23x+cos^24x=2\)
\(\Leftrightarrow2cos^2x+2cos^22x+2cos^23x+2cos^24x=4\)
\(\Leftrightarrow cos2x+cos4x+cos6x+cos8x=0\)
\(\Leftrightarrow2cos5x.cos3x+2cos5x.cosx=0\)
\(\Leftrightarrow cos5x\left(cos3x+cosx\right)=0\)
\(\Leftrightarrow2cos5x.cos2x.cosx=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos5x=0\\cos2x=0\\cosx=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}5x=\dfrac{\pi}{2}+k\pi\\2x=\dfrac{\pi}{2}+k\pi\\x=\dfrac{\pi}{2}+k\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{10}+\dfrac{k\pi}{5}\\x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\\x=\dfrac{\pi}{2}+k\pi\end{matrix}\right.\)

\(a)A\ge\dfrac{x-\sqrt{x}-3}{\sqrt[]{x}}\Leftrightarrow\dfrac{\sqrt{x}-4}{\sqrt{x}}\ge\dfrac{x-\sqrt{x}-3}{\sqrt{x}}\)
\(\Leftrightarrow\sqrt{x}-4\ge x-\sqrt{x}-3\)
\(\Leftrightarrow x-2\sqrt{x}+1\le0\)
\(\Leftrightarrow(\sqrt{x}-1)^2\le0\)
\(\Leftrightarrow\sqrt{x}-1=0\Leftrightarrow\sqrt{x}=1\Leftrightarrow x=1\left(tm\right)\)
\(b)ĐKXĐ:x>0;x\ne4\)
\(B=\dfrac{x+2\sqrt{x}-10}{x-2\sqrt{x}}+\dfrac{\sqrt{x}-1}{\sqrt{x}-2}-\dfrac{\sqrt{x}+2}{\sqrt{x}}\)
\(=\dfrac{x+2\sqrt{x}-10}{\sqrt{x}\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}(\sqrt{x}-1)}{\sqrt{x}\left(\sqrt{x}-2\right)}-\dfrac{(\sqrt{x}+2)(\sqrt{x}-2)}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x+2\sqrt{x}-10+x-\sqrt{x}-x+4}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x+\sqrt{x}-6}{\sqrt{x}\left(\sqrt{x}-2\right)}=\dfrac{(\sqrt{x}+3)\left(\sqrt{x}-2\right)}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
\(=\dfrac{\sqrt{x}+3}{\sqrt{x}}\left(đpcm\right)\)
\(c)\dfrac{A}{B}=\dfrac{\sqrt{x}-4}{\sqrt{x}+3}\Rightarrow\left|\dfrac{A}{B}\right|=\dfrac{\left|\sqrt{x}-4\right|}{\sqrt{x}+3}\left(vì\sqrt{x}+3>0\right)\)
Xét các TH:
\(TH1:\sqrt{x}-4< 0\Leftrightarrow\sqrt{x}< 4\Leftrightarrow x< 16\left(1\right)\)
\(\Rightarrow\left|\dfrac{A}{B}\right|=\dfrac{4-\sqrt{x}}{\sqrt{x}+3}\)
\(\left|\dfrac{A}{B}\right|>\dfrac{A}{B}\Leftrightarrow\dfrac{4-\sqrt{x}}{\sqrt{x}+3}>\dfrac{\sqrt{x}-4}{\sqrt{x}+3}\)
\(\Leftrightarrow4-\sqrt{x}>\sqrt{x}-4\Leftrightarrow2\sqrt{x}< 8\Leftrightarrow\sqrt{x}< 4\)
\(\Leftrightarrow x< 16\left(2\right)\)
Từ (1)(2) suy ra x<16 suy ra x lớn nhất bằng 15
\(TH2:\sqrt{x}-4\ge0.\) Giai tương tự TH1 suy ra loại

a, đkxđ: \(x\ge0\)
\(A=\dfrac{\sqrt{x}}{\sqrt{x}+3}=\dfrac{1}{4}\Leftrightarrow\sqrt{x}+3=4\sqrt{x}\Leftrightarrow3=3\sqrt{x}\Leftrightarrow\sqrt{x}=1\Leftrightarrow\left(\sqrt{x}\right)^2=1^2\Leftrightarrow x=1\)
b,
\(B=\dfrac{2\sqrt{x}-2}{x-2\sqrt{x}+1}+\dfrac{\sqrt{x}+1}{\sqrt{x}-1}=\dfrac{2\sqrt{x}-2}{\left(\sqrt{x}-1\right)^2}+\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)^2}=\dfrac{2\sqrt{x}-2+x-1}{\left(\sqrt{x}-1\right)^2}=\dfrac{\left(\sqrt{x}+1\right)^2-4}{\left(\sqrt{x}-1\right)^2}=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-1\right)^2}=\dfrac{\sqrt{x}+3}{\sqrt{x}-1}\)
c,
\(A.B< 0\Leftrightarrow\dfrac{\sqrt{x}}{\sqrt{x}+3}.\dfrac{\sqrt{x}+3}{\sqrt{x}-1}< 0\Leftrightarrow\dfrac{\sqrt{x}}{\sqrt{x}-1}< 0\)
do \(\sqrt{x}\ge0\) mà \(\frac{\sqrt{x}}{\sqrt{x}-1}<0\Leftrightarrow \sqrt{x}-1<0\Leftrightarrow \sqrt{x}<1\Leftrightarrow x<1\)

2:
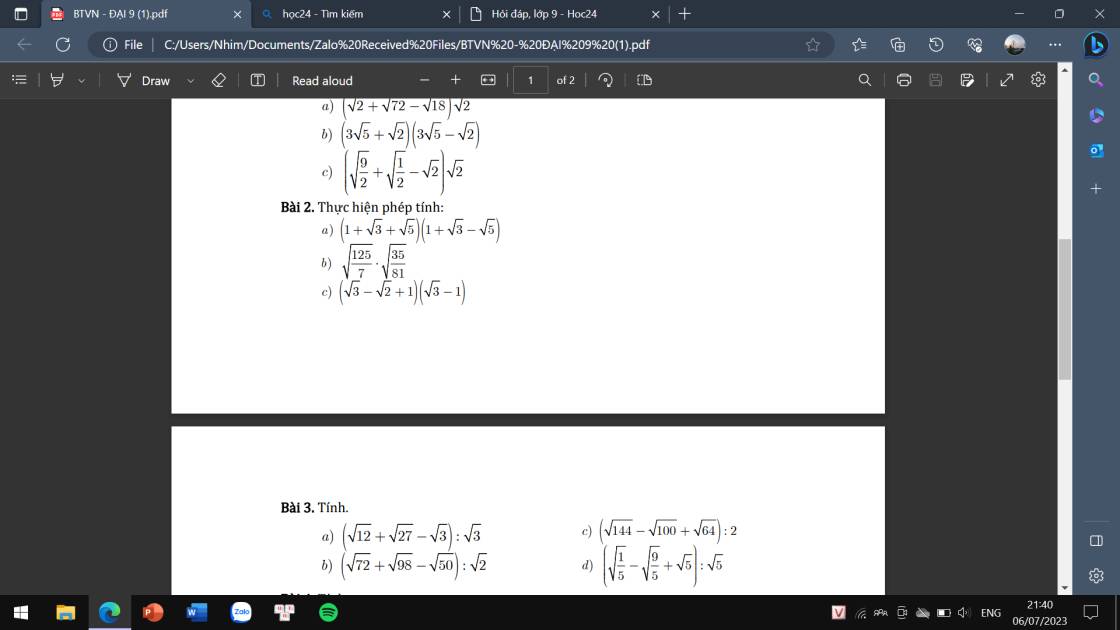
a: =(1+căn 3)^2-5
=4+2căn 3-5
=2căn 3-1
b: \(=\sqrt{\dfrac{125}{7}\cdot\dfrac{35}{81}}=\sqrt{\dfrac{625}{81}}=\dfrac{25}{9}\)
c: \(=\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)-\sqrt{6}+\sqrt{2}\)
=2-căn 6+căn 2
3:
a: \(=\dfrac{2\sqrt{3}+3\sqrt{3}-\sqrt{3}}{\sqrt{3}}=2+3-1=5\)
b: \(=\dfrac{6\sqrt{2}+7\sqrt{2}-5\sqrt{2}}{\sqrt{2}}=13-5=8\)
c: \(=\dfrac{12-10+8}{2}=5\)
d: \(=\sqrt{\dfrac{1}{5}:5}-\sqrt{\dfrac{9}{5}:5}+\sqrt{5:5}\)
=1/5-3/5+1
=3/5

Gọi \(M\left(x;y\right)\) là 1 điểm bất kì trên (E) \(\Rightarrow\dfrac{x^2}{16}+\dfrac{y^2}{9}=1\) (1)
Gọi \(M'\left(x';y'\right)\) là ảnh của M qua phép tịnh tiến \(\overrightarrow{v}\Rightarrow M'\in\left(E'\right)\) với (E') là ảnh của (E) qua phép tịnh tiến nói trên
\(\left\{{}\begin{matrix}x'=x+3\\y'=y-2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=x'-3\\y=y'+2\end{matrix}\right.\)
Thế vào (1):
\(\dfrac{\left(x'-3\right)^2}{16}+\dfrac{\left(y'+2\right)^2}{9}=1\)
Hay pt (E') có dạng: \(\dfrac{\left(x-3\right)^2}{16}+\dfrac{\left(y+2\right)^2}{9}=1\)