Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A.
Gọi N, Q lần lượt là trung điểm của AB, CD ⇒ M N ⊥ A B M Q ⊥ A B .
Qua N kẻ đường thẳng song song với BC, cắt SC tại P.
Suy ra thiết diện của mặt phẳng α và hình chóp là MNPQ.
Vì MQ là đường trung bình của hình tháng ABCD ⇒ M Q = 3 a 2 .
MN là đường trung bình của tam giác SAB ⇒ M N = S A 2 = a .
NP là đường trung bình của tam giác SBC ⇒ N P = B C 2 = a 2 .
Vậy diện tích hình thang MNPQ là S M N P Q = M N . N P + M Q 2 = a 2 a 2 + 3 a 2 = a 2 .
a) Gọi I là giao điểm của mặt phẳng (α) với cạnh SC. Ta có: (α) ⊥ SC, AI ⊂ (α) ⇒ SC ⊥ AI. Vậy AI là đường cao của tam giác vuông SAC. Trong mặt phẳng (SAC), đường cao AI cắt SO tại K và AI ⊂ (α), nên K là giao điểm của SO với (α).
b) Ta có 
⇒ BD ⊥ SC
Mặt khác BD ⊂ (SBD) nên (SBD) ⊥ (SAC).
Vì BD ⊥ SC và (α) ⊥ SC nhưng BD không chứa trong (α) nên BD // (α)
Ta có K = SO ∩ (α) và SO thuộc mặt phẳng (SBD) nên K là một điểm chung của (α) và (SBD).
Mặt phẳng (SBD) chứa BD // (α) nên cắt theo giao tuyến d // BD. Giao tuyến này đi qua K là điểm chung của (α) và (SBD).
Gọi M và N lần lượt là giao điểm của d với SB và SD. Ta được thiết diện là tứ giác AIMN vuông góc với SC và đường chéo MN song song với BD.
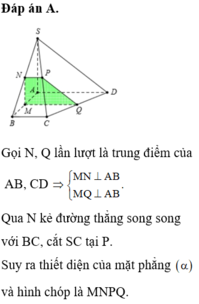
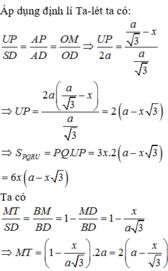
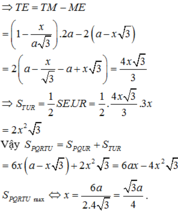
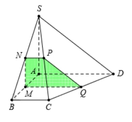
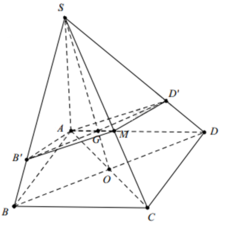
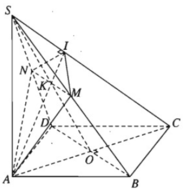
Gọi (α) là mặt phẳng qua O song song với AB và SC.
AB // (α) nên (α) cắt mp(ABCD) theo giao tuyến qua O và song song với AB. Gọi M, N lần lượt là giao điểm của đường thẳng qua O song song AB với BC và AD.
Trong mặt phẳng (SAC) kẻ OP // SC (P ϵ AS) (α) cắt mp(SAB) theo giao tuyến PQ // AB (Q ϵ SB)
Thiết diện cần tìm là tứ giác MNPQ.
Tứ giác MNPQ có PQ // MN nên MNPQ là hình thang.