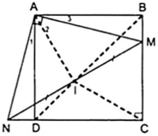
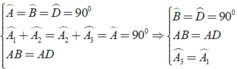cho hình vuông ABCD, M là điểm nằm giữa B,C kẻ AN⊥AM,AP⊥MN (N,P∈CD)
a) Chứng minh ΔAMN vuông cân và \(AN^2\)=NC.NP
b) tính \(P_{CMP}\)và \(P_{ABCD}\)
c) gọi Q là giao tia AM,DC. Chứng minh \(\dfrac{1}{AM^2}+\dfrac{1}{AQ^2}\)không đổi khi điểm M thay đổi trên BC.