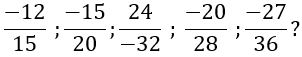K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TT
0
Những câu hỏi liên quan
NK
1
23 tháng 9 2023
Bạn cần bài nào ạ? Nếu bạn cần giúp tất cả thì bạn tách ra từng CH khác nhau nhé!
NP
0
PT
2
V
violet
Giáo viên
29 tháng 4 2016
Bạn phải có bảng giá trị thì mới vẽ được.
Nó giống như vẽ đồ thị ấy.
30 tháng 4 2016
- Bước 1: Nghiên cứu kỹ câu hỏi để xác định dạng biểu đồ thích hợp (xem trong mục cách lựa chọn và vẽ biểu đồ đã trình bày ở phần trước).
- Bước 2. Kẻ trục toạ độ. Cần chú ý:
Trục đứng (ghi mốc giá trị), trục ngang (ghi mốc thời gian). Chọn độ lớn của các trục hợp lý, đảm bảo tính mỹ thuật, dễ quan sát (đặc biệt là khi các đường biểu diễn quá xít nhau). Nếu xảy ra trường hợp các đại lượng có giá trị quá lớn, quá lẻ (hoặc có từ 3 đại lượng trở lên...). Nên chuyển các đại lượng tuyệt đối thành đại lượng tương đối (%) để vẽ. Trong trường hợp này, biểu đồ chí có 1 trục đứng và 1 trục ngang. Ở đầu các trục đứng phải ghi danh số (ví dụ: triệu ha, triệu tấn, triệu người, tỉ USD ...). Ở đầu trục ngang ghi danh số (ví dụ: năm). Ở 2 đầu cột phải có chiều mũi tên chỉ chiều tăng lên của giá trị và thời gian ( ).
Trên trục ngang (X) phải chia các mốc thời gian phù hợp với tỉ lệ khoảng cách các năm. Trên trục đứng (Y), phải ghi mốc giá trị cao hơn mốc giá trị cao nhất của chuỗi số liệu. Phải ghi rõ gốc toạ độ (gốc tọa độ có thể là (0), cũng có trường hợp gốc tọa độ khác (0), nếu có chiều âm (-) thì phải ghi rõ. Với dạng biểu đồ có 2 đại lượng khác nhau: Kẻ 2 trục (Y) và (Y’) đứng ở 2 mốc thời gian đầu và cuối.
- Bước 3: Xác định các đỉnh: Căn cứ vào số liệu, đối chiếu với các mốc trên trục (Y) và (X) để xác định toạ độ các đỉnh. Nếu là biểu đồ có từ 2 đường trở lên thì các đỉnh nên vẽ theo ký hiệu khác nhau (ví dụ: ●, ♦, ○). Ghi số liệu trên các đỉnh. Kẻ các đoạn thẳng nối các đỉnh để thành đường biểu diễn.
- Bước 4: Hoàn thiện phần vẽ: Lập bảng chú giải (nên có khung). Ghi tên biểu đồ (ở trên, hoặc dưới), tên biểu đồ phải ghi rõ 3 thành phần: “Biểu đồ thể hiện vấn đề gì? ở đâu? thời gian nào?”
- Bước 5:Phân tích và nhận xét (xem trong nội dung đã trình bày ở phần trước)
?
6 tháng 9 2021
a: \(-\dfrac{15}{20};\dfrac{24}{-32};-\dfrac{27}{36}\)
D
25 tháng 1 2022
23.
- Gọi E là trung điểm AB.
- Xét tam giác ABH vuông tại H có:
\(\widehat{ABH}+\widehat{BAH}=90^0\) (kề phụ)
=>\(\widehat{ABH}+30^0=90^0\)
=>\(\widehat{ABH}=90^0-30^0=60^0\).
- Xét tam giác ABH vuông tại H có:
HE là trung tuyến ứng với cạnh huyền AB (E là trung điểm AB).
=>\(HE=BE=\dfrac{1}{2}AB\).
=>Tam giác BEH cân tại E.
Mà \(\widehat{EBH}=60^0\)(cmt)
=>Tam giác BEH đều.
=>\(BH=HE=BE=\dfrac{1}{2}AB\)
=>AB=2.BH=2.3,1=6,2 (cm).
* SABCD=6,2.3,1=19,22 (cm2).
24.- Ta có: SABCD=\(\dfrac{1}{2}AC.BD\)=48m2
=>AC.BD=24m2.
- Ta có: \(\dfrac{AC}{BD}=\dfrac{2}{3}\)(gt) =>AC=\(\dfrac{2}{3}BD\)
=>\(\dfrac{2}{3}BD^2\)=24 =>BD=6cm.
=>AC=\(\dfrac{2}{3}.6=4\)(cm)
25 tháng 1 2022
a: \(S=\dfrac{10\cdot24}{2}=24\cdot5=120\left(cm^2\right)\)
b: Cạnh của hình thoi là:
\(\sqrt{5^2+12^2}=13\left(cm\right)\)
Chu vi là 13x4=52(cm)
NT
3
12 tháng 5 2022
Para 1 - b
Para 2 - a
Para 3 - c
T - F - T - T - NG
1 B
2 A
3 D
4 D
5 A
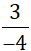