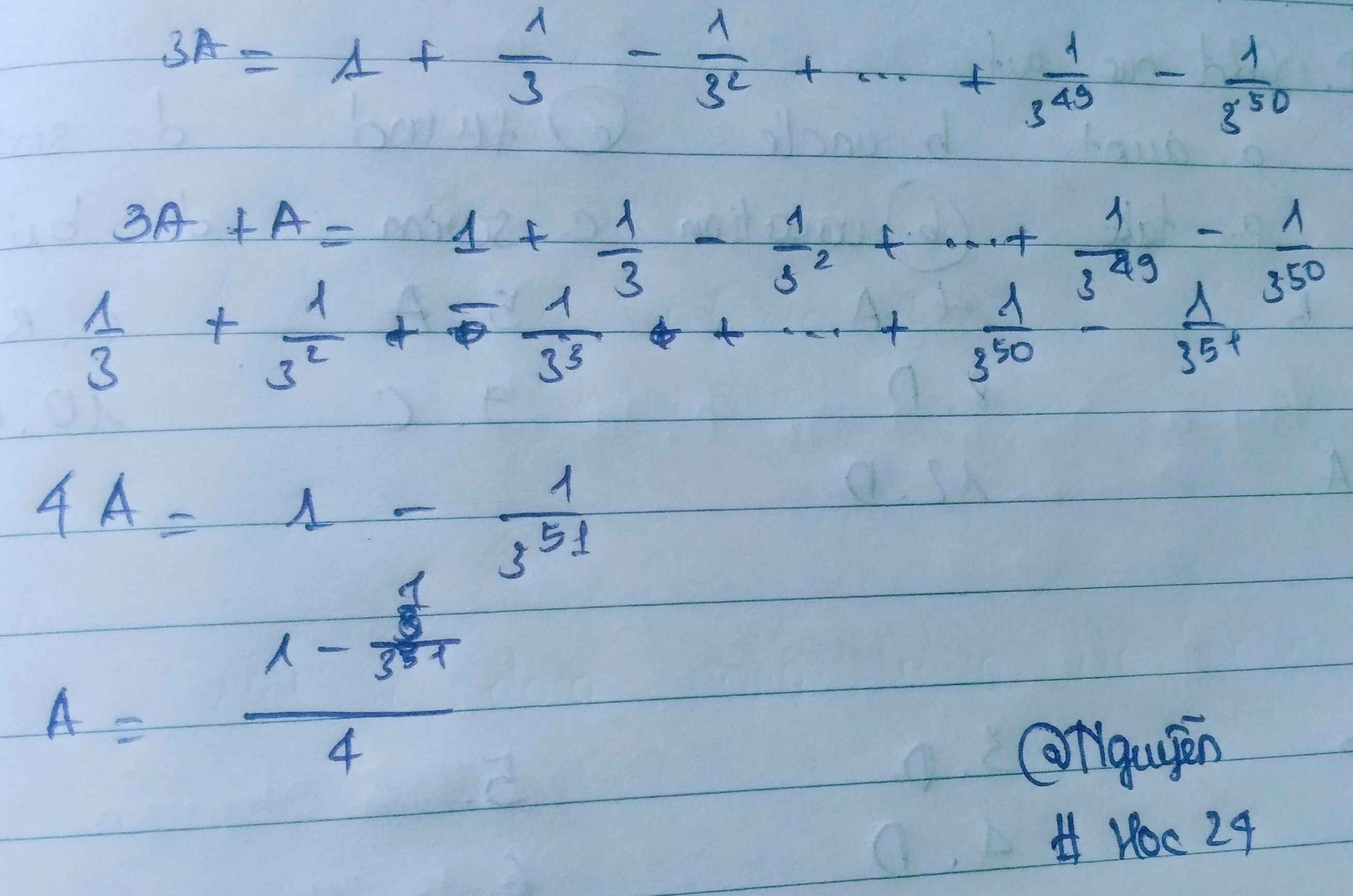B = \(-\dfrac{1}{3}+\dfrac{1}{3^2}-\dfrac{1}{3^3}+...+\dfrac{1}{3^{50}}-\dfrac{1}{3^{51}}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(B=\dfrac{1}{3}+\dfrac{1}{3^2}-\dfrac{1}{3^3}+...+\dfrac{1}{3^{50}}-\dfrac{1}{3^{51}}\)
\(=\dfrac{1}{\left(-3\right)}+\dfrac{1}{\left(-3\right)^2}+\dfrac{1}{\left(-3\right)^3}+...+\dfrac{1}{\left(-3\right)^{50}}+\dfrac{1}{\left(-3\right)^{51}}-\dfrac{1}{3}\)
\(=\dfrac{1}{\left(3\right)^2}+\dfrac{1}{\left(3\right)^3}+...+\dfrac{1}{\left(-3\right)^{51}}+\dfrac{1}{\left(-3\right)^{52}}\)
\(\Rightarrow\dfrac{4}{3}B=\dfrac{1}{-3}-\dfrac{1}{\left(-3\right)^{52}}=\dfrac{-3^{51}-1}{3^{52}}\Rightarrow B=\dfrac{-3^{51}-1}{4.3^{51}}\)

\(3B=-1+\dfrac{1}{3}-\dfrac{1}{3^2}+..+\dfrac{1}{49}-\dfrac{1}{3^{50}}\)
3B+ B = -1 - \(\dfrac{1}{3^{51}}\)
4B= \(-1-\dfrac{1}{3^{51}}\)
B = \(\dfrac{-1-\dfrac{1}{3^{51}}}{4}\)

Lời giải:
a)
\(\frac{\frac{2}{3}-\frac{2}{5}+\frac{2}{7}-\frac{2}{9}+\frac{2}{11}}{\frac{8}{3}-\frac{8}{5}+\frac{8}{7}-\frac{8}{9}+\frac{8}{11}}=\frac{2\left(\frac{1}{3}-\frac{1}{5}+\frac{1}{7}-\frac{1}{9}+\frac{1}{11}\right)}{8\left(\frac{1}{3}-\frac{1}{5}+\frac{1}{7}-\frac{1}{9}+\frac{1}{11}\right)}\) \(=\frac{2}{8}=\frac{1}{4}\)
b)
\(\left(\frac{1}{2}-1\right)\left(\frac{1}{3}-1\right)\left(\frac{1}{4}-1\right)....\left(\frac{1}{50}-1\right)\left(\frac{1}{51}-1\right)\)
\(=\frac{1-2}{2}.\frac{1-3}{3}.\frac{1-4}{4}....\frac{1-50}{50}.\frac{1-51}{2}=\frac{(-1)(-2)(-3)...(-49)(-50)}{2.3.4....50.51}\)
\(=\frac{(-1)^{50}.1.2.3....49.50}{2.3.4...50.51}=\frac{1}{51}\)

a/ Đặt :
\(A=\dfrac{1}{3}+\dfrac{1}{3^2}+.........+\dfrac{1}{3^{50}}\)
\(\Leftrightarrow3A=1+\dfrac{1}{3}+\dfrac{1}{3^2}+.......+\dfrac{1}{3^{49}}\)
\(\Leftrightarrow3A-A=\left(1+\dfrac{1}{3}+....+\dfrac{1}{3^{49}}\right)-\left(\dfrac{1}{3}+\dfrac{1}{3^2}+....+\dfrac{1}{3^{50}}\right)\)
\(\Leftrightarrow2A=1-\dfrac{1}{3^{50}}\)
còn sao nx thì mk chịu =.=

\(A=\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{50}}\)
\(3.A=1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{49}}\)
\(2A=3A-A=1-\dfrac{1}{3^{49}}\)
\(\Rightarrow A=\dfrac{1-\dfrac{1}{3^{50}}}{2}\)
\(B=\dfrac{5}{3}+\dfrac{5}{3^2}+...+\dfrac{5}{3^{50}}=5\left(\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{50}}\right)\)
Căn cứ vào câu A thì các trong ngặc bằng \(\dfrac{1-\dfrac{1}{3^{50}}}{2}\)
suy ra \(B=\dfrac{5\left(1-\dfrac{1}{3^{50}}\right)}{2}\)
tick mik nha

a) Ta có: \(\dfrac{-5}{18}+\dfrac{32}{45}-\dfrac{9}{10}\)
\(=\dfrac{-25}{90}+\dfrac{64}{90}-\dfrac{81}{90}\)
\(=\dfrac{-42}{90}=-\dfrac{7}{15}\)
b) Ta có: \(\left(-\dfrac{1}{4}+\dfrac{51}{33}-\dfrac{5}{3}\right)-\left(-\dfrac{15}{12}+\dfrac{6}{11}-\dfrac{42}{29}\right)\)
\(=\dfrac{-1}{4}+\dfrac{17}{11}-\dfrac{5}{3}+\dfrac{5}{4}-\dfrac{6}{11}+\dfrac{42}{29}\)
\(=\dfrac{-5}{3}+\dfrac{42}{29}\)
\(=\dfrac{-145}{87}+\dfrac{126}{87}=\dfrac{-19}{87}\)
c) Ta có: \(1-\dfrac{1}{2}+2-\dfrac{2}{3}+3-\dfrac{3}{4}+4-\dfrac{1}{4}-3-\dfrac{1}{3}-2-\dfrac{1}{2}-1\)
\(=\left(1-1\right)-\left(\dfrac{1}{2}+\dfrac{1}{2}\right)+\left(2-2\right)-\left(\dfrac{2}{3}+\dfrac{1}{3}\right)+\left(3-3\right)-\left(\dfrac{3}{4}+\dfrac{1}{4}\right)+4\)
\(=-1-1-1+4\)
=1
a) Ta có: −518+3245−910−518+3245−910
=−2590+6490−8190=−2590+6490−8190
=−4290=−715=−4290=−715
b) Ta có: (−14+5133−53)−(−1512+611−4229)(−14+5133−53)−(−1512+611−4229)
=−14+1711−53+54−611+4229=−14+1711−53+54−611+4229
=−53+4229=−53+4229
=−14587+12687=−1987=−14587+12687=−1987
c) Ta có: 1−12+2−23+3−34+4−14−3−13−2−12−11−12+2−23+3−34+4−14−3−13−2−12−1
=(1−1)−(12+12)+(2−2)−(23+13)+(3−3)−(34+14)+4=(1−1)−(12+12)+(2−2)−(23+13)+(3−3)−(34+14)+4
=−1−1−1+4=−1−1−1+4
=1

Bài 1: Tìm x biết:
a) \(\dfrac{6}{5}-2\left|1-3x\right|=1\dfrac{2}{3}\)
\(2\left|1-3x\right|=\dfrac{6}{5}-1\dfrac{2}{3}\)
\(2\left|1-3x\right|=\dfrac{-7}{15}\)
\(\left|1-3x\right|=\dfrac{-7}{15}:2\)
\(\left|1-3x\right|=\dfrac{-7}{30}\)
\(\left|1-3x\right|\in N\) nhưng \(\dfrac{-7}{30}\notin N\)
\(\Rightarrow x=\varnothing\)
b) \(\left(2,8x+50\right):\dfrac{-3}{2}=51\)
\(\left(2,8x+50\right)=51.\dfrac{-3}{2}\)
\(2,8x+50=\dfrac{-153}{2}\)
\(2,8x=\dfrac{-153}{2}-50\)
\(2,8x=\dfrac{-253}{2}\)
\(x=\dfrac{-253}{2}:2,8\)
\(x=\dfrac{-1265}{28}\)
c) \(\dfrac{x-2}{-2}=\dfrac{x+4}{3}\)
\(\Rightarrow\left(x-2\right).3=-2.\left(x+4\right)\)
\(x.3-2.3=\left(-2\right).x+\left(-2\right).4\)
\(3x-6=\left(-2\right)x+\left(-8\right)\)
\(3x-\left(-2\right)x=6+\left(-8\right)\)
\(5x=-2\)
\(x=\left(-2\right):5\)
\(x=\dfrac{-2}{5}\)
d) \(4\left(3-2x\right)-5\left(x-1\right)=12\)
\(4.3-4.2x-5x+5.1=12\)
\(12-8x-5x+5=12\)
\(12+\left(-8\right)x+\left(-5\right)x+5=12\)
\(12+\left(-13\right)x+5=12\)
\(\left(-13\right)x=12-12-5\)
\(\left(-13\right)x=-5\)
\(x=\left(-5\right):\left(-13\right)\)
\(x=\dfrac{5}{13}\)
Bài 2: Chứng minh:
\(\dfrac{1}{3^2}+\dfrac{1}{4^2}+\dfrac{1}{5^2}+...+\dfrac{1}{100^2}< \dfrac{1}{2}\)
\(\dfrac{1}{3^2}+\dfrac{1}{4^2}+\dfrac{1}{5^2}+...+\dfrac{1}{100^2}< \dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{99.100}\)
\(=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{99}-\dfrac{1}{100}=\dfrac{1}{2}-\dfrac{1}{100}< \dfrac{1}{2}\)
\(\Rightarrow\dfrac{1}{3^2}+\dfrac{1}{4^2}+\dfrac{1}{5^2}+...+\dfrac{1}{100^2}< \dfrac{1}{2}\) (đpcm)

\(B=\dfrac{1}{49}+\dfrac{2}{48}+\dfrac{3}{47}+...+\dfrac{48}{2}+\dfrac{49}{1}\)
\(B=\left(\dfrac{1}{49}+1\right)+\left(\dfrac{2}{48}+1\right)+\left(\dfrac{3}{47}+1\right)+...+\left(\dfrac{48}{2}+1\right)+\dfrac{49}{1}\)
\(B=\left(\dfrac{50}{49}+\dfrac{50}{49}+\dfrac{50}{48}+\dfrac{50}{47}+...+\dfrac{50}{2}\right)+1\)
\(B=\dfrac{50}{50}+\dfrac{50}{49}+\dfrac{50}{49}+\dfrac{50}{48}+\dfrac{50}{47}+...+\dfrac{50}{2}\)
\(B=50\left(\dfrac{1}{50}+\dfrac{1}{49}+\dfrac{1}{48}+...+\dfrac{1}{2}\right)\)
\(\Rightarrow\dfrac{A}{B}=\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{49}+\dfrac{1}{50}}{50\left(\dfrac{1}{50}+\dfrac{1}{49}+\dfrac{1}{48}+...+\dfrac{1}{2}\right)}=\dfrac{1}{50}\)

Câu b hướng làm đó là tách con 1/3 và 1/2 ra thành 50 phân số giống nhau. E tách 1/3=50/150 rồi so sánh 1/101, 1/102,...,1/149 với 1/150. Còn vế sau 1/2=50/100 tách tương tự rồi so sánh thôi
2a.
$\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{50^2}$
$< \frac{1}{1.2}+\frac{1}{2.3}+....+\frac{1}{49.50}$
$=\frac{2-1}{1.2}+\frac{3-2}{2.3}+...+\frac{50-49}{49.50}$
$=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+....+\frac{1}{49}-\frac{1}{50}$
$=1-\frac{1}{50}< 1$ (đpcm)