
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,y'=\left(\dfrac{1}{2x+3}\right)'=-\dfrac{2}{\left(2x+3\right)^2}\\ \Rightarrow y''=\dfrac{2\cdot\left[\left(2x+3\right)^2\right]'}{\left(2x+3\right)^4}=\dfrac{8}{\left(2x+3\right)^3}\\ b,y'=\left(log_3x\right)'=\dfrac{1}{xln3}\\ \Rightarrow y''=-\dfrac{1}{x^2ln3}\\ c,y'=\left(2^x\right)'=2^x\cdot ln2\\ \Rightarrow y''=2^x\cdot\left(ln2\right)^2\)

Đáp án C
y ' = 1. x 2 + 1 + x . 2 x 2 x 2 + 1 = x 2 + 1 + x 2 x 2 + 1 = ( x 2 + 1 ) + x 2 x 2 + 1 = 2 x 2 + 1 x 2 + 1
y " = 4 x . x + 2 1 − ( 2 x 2 + 1 ) . x x 2 + 1 x 2 + 1 = 4 x ( x 2 + 1 ) − ( 2 x 2 + 1 ) . x ( x 2 + 1 ) . x 2 + 1 = 2 x 3 + 3 x ( x 2 + 1 ) . x 2 + 1

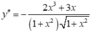
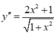
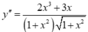
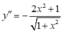
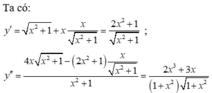
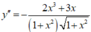
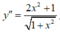
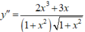
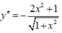
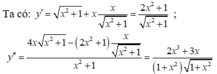
\(y=\frac{x^2+1}{x-1}=\frac{x^2-1+2}{x-1}=x+1+\frac{2}{x-1}\)
\(y'=1-\frac{2}{\left(x-1\right)^2}\)
\(y''=\frac{4}{\left(x-1\right)^3}\)