1. Cho ΔA'B'C' đồng dạng Δ ABC theo tỉ số k=\(\dfrac{1}{3}\). Biết AB=7, AC=10, BC=9. Tính A'B', A'C', B'C'.
2. Cho ΔA'B'C' đồng dạng Δ ABC, biết góc A=30o, góc B=50o. Tính góc C,A', B', C'.
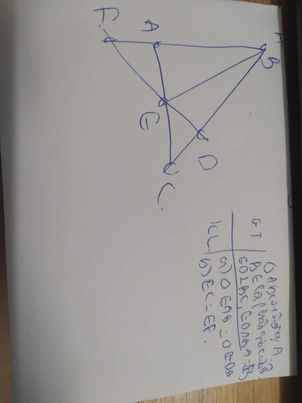
3. Cho Δ ABC, lấy M, N lần lượt trên AB, AC sao cho MN//BC. CM: ΔAMN đồng dạng ΔABC

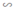
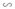
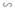 ΔA''B''C'' theo tỉ số đồng dạng k
ΔA''B''C'' theo tỉ số đồng dạng k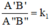
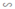 ΔABC theo tỉ số đồng dạng k
ΔABC theo tỉ số đồng dạng k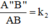
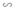 ΔA''B''C''; ΔA''B''C''
ΔA''B''C''; ΔA''B''C'' 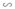 ΔABC
ΔABC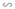 ΔABC (theo tính chất 3)
ΔABC (theo tính chất 3)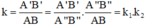

Câu 3:
Xét ΔAMN và ΔABC có
AM/AB=AN/AC
\(\widehat{A}\) chung
DO đó: ΔAMN\(\sim\)ΔABC