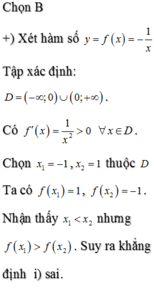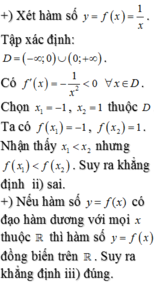Cho hàm số y=f(x)=2/x.3. CMR với mọi x thuộc R thì f(x)=f(-x).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DD
Đoàn Đức Hà
Giáo viên
24 tháng 7 2021
\(f\left(x\right)+3f\left(\frac{1}{x}\right)=x^2\)
Thế \(x=2\)ta được:
\(f\left(2\right)+3f\left(\frac{1}{2}\right)=4\)
Thế \(x=\frac{1}{2}\)ta được:
\(f\left(\frac{1}{2}\right)+3f\left(2\right)=\frac{1}{4}\)
Ta có hệ phương trình:
\(\hept{\begin{cases}f\left(2\right)+3f\left(\frac{1}{2}\right)=4\\3f\left(2\right)+f\left(\frac{1}{2}\right)=\frac{1}{4}\end{cases}}\Leftrightarrow\hept{\begin{cases}f\left(2\right)=-\frac{13}{32}\\f\left(\frac{1}{2}\right)=\frac{47}{32}\end{cases}}\)
15 tháng 12 2021
Làm được rồi , mọi người đừng làm nữa :>>>>>>>>>
Q
15 tháng 1 2018
a) Thay f(3) vào hàm số ta có :
y=f(3)=4.32-5=31
Thay f(-1/2) vào hàm số ta có :
y=f(-1/2)=4.(-1/2)2-5=-4
b) Thay x=-1 vào hàm số ta có : 4.(-1)2-5=-1
=> f(-1) với x=-1
DM
0
18 tháng 2 2017
\(x=2\Rightarrow f\left(2\right)+3.f\left(\frac{1}{2}\right)=4\)
\(x=\frac{1}{2}\Rightarrow f\left(\frac{1}{2}\right)+3.f\left(2\right)=\frac{1}{4}\)
\(\Rightarrow f\left(2\right)=\frac{47}{32}\)
18 tháng 2 2017
kết quả nhanh nhất
= 47/32
h mk nha bn hiền
chúc bn học giỏi
AH
Akai Haruma
Giáo viên
9 tháng 8 2021
Bài 1:
Cho $y=0$ thì: $f(x^3)=xf(x^2)$
Tương tự khi cho $x=0$
$\Rightarrow f(x^3-y^3)=xf(x^2)-yf(y^2)=f(x^3)-f(y^3)$
$\Rightarrow f(x-y)=f(x)-f(y)$ với mọi $x,y\in\mathbb{R}$
Cho $x=0$ thì $f(-y)=0-f(y)=-f(y)$
Cho $y\to -y$ thì: $f(x+y)=f(x)-f(-y)=f(x)--f(y)=f(x)+f(y)$ với mọi $x,y\in\mathbb{R}$
Đến đây ta có:
$f[(x+1)^3+(x-1)^3]=f(2x^3+6x)=f(2x^3)+f(6x)$
$=2f(x^3)+6f(x)=2xf(x^2)+6f(x)$
$f[(x+1)^3+(x-1)^3]=f[(x+1)^3-(1-x)^3]$
$=(x+1)f((x+1)^2)-(1-x)f((1-x)^2)$
$=(x+1)f(x^2+2x+1)+(x-1)f(x^2-2x+1)$
$=(x+1)[f(x^2)+2f(x)+f(1)]+(x-1)[f(x^2)-2f(x)+f(1)]$
$=2xf(x^2)+4f(x)+2xf(1)$
Do đó:
$2xf(x^2)+6f(x)=2xf(x^2)+4f(x)+2xf(1)$
$2f(x)=2xf(1)$
$f(x)=xf(1)=ax$ với $a=f(1)$