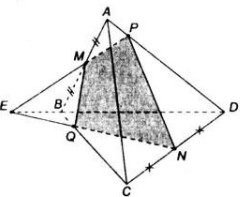
Cho tứ diện ABCD Gọi M N lần lượt là trung điểm của các cạnh BC và AC Trên cạnh BP lấy điểm P sao cho DP=2PB
a) xác định giao tuyến của mặt phẳng (MNP )và mặt phẳng (ABD) b) trên cạnh AD lấy điểm Q sao cho DQ=2QA. Chứng minh PQ song song với mặt phẳng (ABC)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 9 2023
Tham khảo:
a) Xét trên mp(BCD): NP cắt CD tại I
I thuộc NP suy ra I nằm trên mp(MNP)
Suy ra giao điểm của CD và mp(MNP) là I
b) Ta có I, M đều thuộc mp(ACD) suy ra IM nằm trên mp(ACD)
I, M đều thuộc mp(MNP) suy ra IM nằm trên mp(MNP)
Do đó, IM là giao tuyến của 2 mp(ACD) và mp(MNP) hay EM là giao tuyến của 2 mp(ACD) và mp(MNP).
CM
11 tháng 4 2019
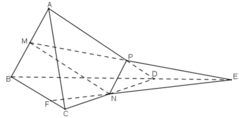
a) Trong mp(ABD): MP không song song với BD nên MP ∩ BD = E.
E ∈ MP ⇒ E ∈ (PMN)
E ∈ BD ⇒ E ∈ (BCD)
⇒ E ∈ (PMN) ∩ (BCD)
Dễ dàng nhận thấy N ∈ (PMN) ∩ (BCD)
⇒ EN = (PMN) ∩ (BCD)
b) Trong mp(BCD) : gọi giao điểm EN và BC là F.
F ∈ EN, mà EN ⊂ (PMN) ⇒ F ∈ (PMN)
⇒ F = (PMN) ∩ BC.
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 1
Trong mp (ACD) kéo dài MN và CD cắt nhau tại I
Trong mp (BCD) nối IQ cắt BD tại J
Áp dụng định lý Menelaus trong tam giác ACD:
\(\dfrac{AM}{MC}.\dfrac{CI}{ID}.\dfrac{DN}{NA}=1\Rightarrow1.\dfrac{CI}{ID}.\dfrac{1}{2}=1\Rightarrow IC=2ID\)
Do \(BC=4BQ\Rightarrow QC+QB=4QB\Rightarrow QC=3QB\)
Menelaus cho tam giác BCD:
\(\dfrac{QC}{QB}.\dfrac{BJ}{JD}.\dfrac{DI}{IC}=1\Rightarrow3.\dfrac{BJ}{JD}.\dfrac{1}{2}=1\Rightarrow\dfrac{BJ}{JD}=\dfrac{2}{3}\)
Menelaus cho tam giác CQI:
\(\dfrac{ID}{DC}.\dfrac{CB}{BQ}.\dfrac{QJ}{JI}=1\Rightarrow1.4.\dfrac{JQ}{JI}=1\Rightarrow\dfrac{JQ}{JI}=\dfrac{1}{4}\)
\(\Rightarrow\dfrac{JB}{JD}+\dfrac{JQ}{JI}=\dfrac{2}{3}+\dfrac{1}{4}=\dfrac{11}{12}\)
Bạn tự vẽ hình nhá
a, \(P\subset BD\in\left(ABD\right)\)
=> P là điểm chung của \(\left(MNP\right)vs\left(ABD\right)\)
Trong tam giác ABC có :
N là trung điểm AC
M là trung diểm BC
=> MN là đường trung bình của tg ABC => MN song song AB
Qua P kẻ (d) song song với AB
vậy giao tuyến 2mp là (d)
b, Vì QD=2QA => A là trung điểm QD
tương tự thì B là trung điểm DP
\(Q\subset AD\in ADB\)
\(P\subset DB\in ABD\)
trong tam giacs AQP có
A là trung điểm DP
B là trung điểm DP
=>AB là đường trung bình tg AQP
=> AB song song QP. mà \(AB\in ABC\)
=> QP song song (ABC)
cảm ơn bạn nha