Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Hình vẽ
Vì E là trung điểm của AD và F là tung điểm cùa AC nên EF là đường trung bình của tam giác ADC và tam giác ABD
Mà P thuộc đường thẳng EF nên EP cũng là đường trung bình của tam giác ABD
Suy ra PD=PB
Vì EF là đường trung bình của tam giác ADC mà Q lại thuộc đường thẳng EQ cắt BC nên
FQ là đường trung bình của tam giác ABC
Suy ra QB=QC
Câu b)
Vì EF là đường trung bình của tam giác ADC nên
\(EF=\frac{1}{2}CD\)
Suy ra CD= 10
Vì FQ là đường trung bình của tam giác ABC nên
\(FQ=\frac{1}{2}\cdot6=3\)
Mà \(EQ=EF+FQ\)
Thay vào ta có \(EQ=5+3=8\)
Ở đây em mới hc lớp 7 thui có j thiếu anh(chị) bổ sung giùm em
Câu 1
Cho 
vuông tại A, D là trung điểm của BC. Gọi M là điểm đối xứng với D qua AB, E là giao điểm của DM và AB. Gọi N là điểm đối xứng với D qua AC, F là giao điểm của DN và AC.
a. Tứ giác AEDF là hình gì? Vì sao?
b. Các tứ giác ADBM, ADCN là hình gì? Vì sao?
câu 2 Cho , D là trung điểm cạnh AB, E là trung điểm cạnh AC. Tính độ dài cạnh BC, biết DE=4cm.
Bài 3: Cho hình thoi ABCD, gọi O là giao điểm cuả hai đường chéo. Vẽ đường thẳng qua B và song song với AC, vẽ đường thẳng qua C và song song với BD, hai đường thẳng đó cắt nhau ở K.
a/Tứ giác OBKC là hình gì? Vì sao?
b/Chứng minh rằng AB=OK
c/Tìm điều kiện của hình thoi ABCD để OBKC là hình vuông ?
Bài 3 Cho tam giác ABC vuông tại A có AB = 6cm , AC = 8cm , M là trung điểm của BC. Tính độ dài AM.
giúp mình với gấp lắm ạ
Thanks trước ạ
xet tam giac ACD co AE=ED ;AS=SC
\(\Rightarrow\)ES song song DC
ma DC song song AB
suy ra EQ song song AB
ma AS=SC
suy ra BQ=QC
b0 de kieu gi day
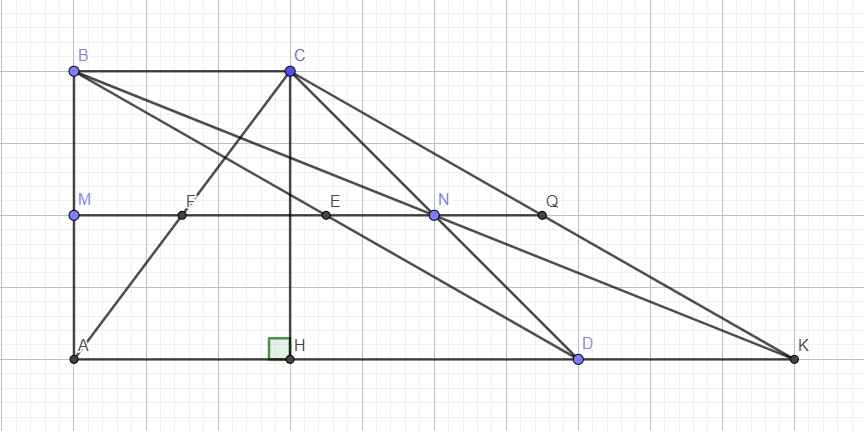
c.
K thuộc AD nên BC song song DK
Áp dụng định lý Talet: \(\dfrac{BN}{KN}=\dfrac{CN}{DN}=1\Rightarrow BN=KN\) hay N là trung điểm BK
\(\Rightarrow\) BCKD là hình bình hành (tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường)
Theo câu b, E, M, N thẳng hàng nên Q nằm trên MN (1)
Mà MN là đường trung bình của hình thang ABCD
\(\Rightarrow MN||AD\Rightarrow MN\perp AB\) (2)
Mà M là trung điểm AB (3)
(2);(3) \(\Rightarrow\) MN là trung trực AB (4)
(1);(4) \(\Rightarrow QB=QA\)
d.
Hạ CH vuông góc AD
Trong tam giác vuông CHK: \(cosKAC=\dfrac{AH}{AC}\Rightarrow AH=AC.cos\widehat{KAC}\)
Pitago: \(CH^2+AH^2=AC^2\)
Do đó: \(CK^2=CH^2+HK^2=CH^2+\left(AK-AH\right)^2=CH^2+AH^2+AK^2-2AK.AH\)
\(=AC^2+AK^2-2AK.AC.cos\widehat{KAC}\) (đpcm)
a: Xét hình thang ABCD có
E là trung điểm của AB
F là trung điểm của DC
Do đó: EF là đường trung bình của hình thang ABCD
Suy ra: EF//AD//BC
Xét tứ giác EFCB có EF//BC
nên EFCB là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên EFCB là hình thang cân
a: Xét ΔIAB và ΔIMD có
góc IAB=góc IMD
góc AIB=góc MID
=>ΔIAB đồng dạng với ΔIMD
=>IA/IM=AB/MD=IB/ID
Xét ΔKAB và ΔKCM có
góc KAB=góc KCM
góc AKB=góc CKM
=>ΔKAB đồng dạng với ΔKCM
=>KA/KC=KB/KM=AB/CM
KB/KM=AB/CM
AI/IM=AB/MD
mà CM=MD
nên KB/KM=AI/IM
=>MI/IA=MK/KB
Xét ΔMAB có MI/IA=MK/KB
nên IK//AB
b: Xét ΔAMC có IK//MC
nên IK/MC=AI/AM
Xét ΔADM có EI//DM
nên EI/DM=AI/AM
Xét ΔBMC có KF//MC
nên KF/MC=BK/BM
Xét ΔMAB có IK//AB
nên AI/AM=BK/BM
=>IK/MC=FK/MC=EI/DM
mà MC=DM
nên IK=FK=EI
