Cho P=x3+x2_11x+m và Q=x-2.Tìm m để P chia hết cho Q.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HH
2
KT
7 tháng 1 2018
Gọi thương của phép chia \(P\)cho \(Q\)là \(A\)
Ta có: \(P=Q.A\)
\(\Leftrightarrow\)\(x^3+x^2-11x+m=\left(x-2\right).A\)
Vì biểu thức luôn đúng với mọi \(x\)nên ta thay \(x=2\)ta được:
\(8+4-22+m=0\)
\(\Leftrightarrow\)\(m-10=0\)
\(\Leftrightarrow\)\(m=10\)
Vậy...
7 tháng 1 2018
To \(P⋮Q\)then \(P=Q.g\left(x\right)\)
<=> P = ( x - 2 ) . g(x)
replace x = 2 to P we have
\(2^3+2^2-11.2+m=8+4-22+m=0\)
\(-12+m=0\)
=> \(m=12\)
Thus , m=12
21 tháng 9 2021
\(a,f\left(x\right):g\left(x\right)=\left(3x^4+9x^3+7x+2\right):\left(x+3\right)\\ =\left[3x^3\left(x+3\right)+7\left(x+3\right)-19\right]:\left(x+3\right)\\ =\left[\left(3x^3+7\right)\left(x+3\right)-19\right]:\left(x+3\right)\\ =3x^3+7.dư.19\)
\(c,\) Để \(k\left(x\right)⋮g\left(x\right)\Leftrightarrow-x^3-5x+2m=\left(x+3\right)\cdot a\left(x\right)\)
Thay \(x=-3\)
\(\Leftrightarrow-\left(-3\right)^3-5\left(-3\right)+2m=0\\ \Leftrightarrow27+15+2m=0\\ \Leftrightarrow2m=-42\\ \Leftrightarrow m=-21\)
23 tháng 2 2023
a: P(x) chia hết cho x-2
=>x^4-2x^3+3x^3-6x^2+12x^2-24x-16x+32+m-2017 chia hết cho x-2
=>m-2017=0
=>m=2017
b: P(x)=x^4+x^3+6x^2-40x+32
P(x)=0
=>x^4-2x^3+3x^3-6x^2+12x^2-24x-16x+32=0
=>(x-2)(x^3+3x^2+12x-16)=0
=>x^3+3x^2+12x-16=0 hoặc x-2=0
=>x^3-x^2+4x^2-4x+16x-16=0 hoặc x-2=0
=>x-1=0 hoặc x=2
=>x=1 hoặc x=2
PT
1
CM
29 tháng 1 2019
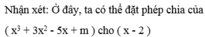
để tìm số dư, rồi cho số dư đó bằng 0, từ đó tìm được giá trị của m.
Mở rộng: Bài toán này ta áp dụng phân tích đa thức thành nhân tử để giải toán
PT
1
7 tháng 1 2023
Bài 2:
x^3+6x^2+12x+m chia hết cho x+2
=>x^3+2x^2+4x^2+8x+4x+8+m-8 chia hết cho x+2
=>m-8=0
=>m=8
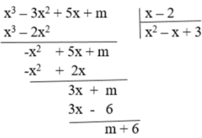
Áp dụng quy tắc HOrner , ta có :
Vậy, để P chia hết cho Q thì : -10 + m = 0
=> m = 10
https://giaibaitapvenha.blogspot.com/2017/12/toan-lop-8-ai-so.html