TT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HH
2
KT
7 tháng 1 2018
Gọi thương của phép chia \(P\)cho \(Q\)là \(A\)
Ta có: \(P=Q.A\)
\(\Leftrightarrow\)\(x^3+x^2-11x+m=\left(x-2\right).A\)
Vì biểu thức luôn đúng với mọi \(x\)nên ta thay \(x=2\)ta được:
\(8+4-22+m=0\)
\(\Leftrightarrow\)\(m-10=0\)
\(\Leftrightarrow\)\(m=10\)
Vậy...
7 tháng 1 2018
To \(P⋮Q\)then \(P=Q.g\left(x\right)\)
<=> P = ( x - 2 ) . g(x)
replace x = 2 to P we have
\(2^3+2^2-11.2+m=8+4-22+m=0\)
\(-12+m=0\)
=> \(m=12\)
Thus , m=12
21 tháng 9 2021
\(a,f\left(x\right):g\left(x\right)=\left(3x^4+9x^3+7x+2\right):\left(x+3\right)\\ =\left[3x^3\left(x+3\right)+7\left(x+3\right)-19\right]:\left(x+3\right)\\ =\left[\left(3x^3+7\right)\left(x+3\right)-19\right]:\left(x+3\right)\\ =3x^3+7.dư.19\)
\(c,\) Để \(k\left(x\right)⋮g\left(x\right)\Leftrightarrow-x^3-5x+2m=\left(x+3\right)\cdot a\left(x\right)\)
Thay \(x=-3\)
\(\Leftrightarrow-\left(-3\right)^3-5\left(-3\right)+2m=0\\ \Leftrightarrow27+15+2m=0\\ \Leftrightarrow2m=-42\\ \Leftrightarrow m=-21\)
23 tháng 2 2023
a: P(x) chia hết cho x-2
=>x^4-2x^3+3x^3-6x^2+12x^2-24x-16x+32+m-2017 chia hết cho x-2
=>m-2017=0
=>m=2017
b: P(x)=x^4+x^3+6x^2-40x+32
P(x)=0
=>x^4-2x^3+3x^3-6x^2+12x^2-24x-16x+32=0
=>(x-2)(x^3+3x^2+12x-16)=0
=>x^3+3x^2+12x-16=0 hoặc x-2=0
=>x^3-x^2+4x^2-4x+16x-16=0 hoặc x-2=0
=>x-1=0 hoặc x=2
=>x=1 hoặc x=2
PT
1
CM
29 tháng 1 2019
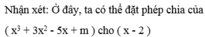
để tìm số dư, rồi cho số dư đó bằng 0, từ đó tìm được giá trị của m.
Mở rộng: Bài toán này ta áp dụng phân tích đa thức thành nhân tử để giải toán
PT
1
7 tháng 1 2023
Bài 2:
x^3+6x^2+12x+m chia hết cho x+2
=>x^3+2x^2+4x^2+8x+4x+8+m-8 chia hết cho x+2
=>m-8=0
=>m=8
TT
0
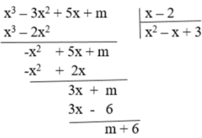
Áp dụng quy tắc HOrner , ta có :
Vậy, để P chia hết cho Q thì : -10 + m = 0
=> m = 10
https://giaibaitapvenha.blogspot.com/2017/12/toan-lop-8-ai-so.html