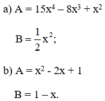Thực hiện phép chia đa thức C= (7x2y3 - 3xy2z + 5x2z3 - 2314):(x3y2 + 3x2yz2- 5yz3+ 4718)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 1 2023
Bài 2:
a: =x(x^2-25)
=x(x-5)(x+5)
b: =x(x-2y)+3(x-2y)
=(x-2y)(x+3)
c: =(2x-3)(4x^2+6x+9)+2x(2x-3)
=(2x-3)(4x^2+8x+9)
17 tháng 8 2021
a: \(10x^3y^2z:\left(-4xy^2z\right)=-\dfrac{5}{2}x^2\)
b: \(32x^2y^3z^4:14y^2z=\dfrac{16}{7}x^2yz^3\)
c: \(25x^4y^5z^3:\left(-3xy^2z\right)=-\dfrac{25}{3}x^3y^3z^2\)
f: \(\left(-35xy^5z\right):\left(-12xy^4\right)=\dfrac{35}{12}yz\)
g: \(x^3y^4:x^3y=y^3\)
h: \(18x^2y^2z:6xyz=3xy\)
19 tháng 12 2021
Bài 1:
a: \(=\dfrac{2x^4-8x^3+2x^2+2x^3-8x^2+2x+18x^2-72x+18+56x-15}{x^2-4x+1}\)
\(=2x^2+2x+18+\dfrac{56x-15}{x^2-4x+1}\)
PT
1
CM
30 tháng 5 2017
a ) 2 1 4 : 3 5 4 = 9 4 : 17 4 = 9 4 . 4 17 = 9 17
b ) − 3 1 7 : − 2 3 14 = − 22 7 : − 31 7 = 22 31
BN
2
PT
1
CM
24 tháng 11 2019
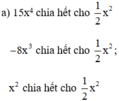
Do đó A = 15x4 - 8x3 + x2 chia hết cho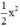 
hay A chia hết cho B.
b) A = x2 - 2x + 1 = (x – 1)2
Vậy A chia hết cho x – 1 hay A chia hết cho B.
N
1
2 tháng 12 2021
\(=\left(x^4-x^3+x^2+x^3-x^2+x+3x^2-3x+3+2018\right):\left(x^2-x+1\right)\\ =\left[\left(x^2-x+1\right)\left(x^2+x+3\right)+2018\right]:\left(x^2-x+1\right)\\ =x^2+x+3\left(\text{dư 2018}\right)\)
HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
Để thực hiện phép chia một đa thức cho một đa thức khác, ta làm như sau:
Bước 1:
- Chia đơn thức bậc cao nhất của đa thức bị chia cho đơn thức bậc cao nhất của đa thức chia.
- Nhân kết quả trên với đa thức chia và đặt tích dưới đa thức bị chia sao cho hai đơn thức có cùng số mũ của biến ở cùng cột.
- Lấy đa thức bị chia trừ đi tích đặt dưới để được đa thức mới.
Bước 2: Tiếp tục quá trình trên cho đến khi nhận được đa thức không hoặc đa thức có bậc nhỏ hơn bậc của đa thức chia.