Cho A = 5 + 52 + 53 + ... + 599 . Tìm số tự nhiên n , biết : 4A + 5 = 5n .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A= 1 + 5 + 52 + 5 3 + ... + 5800
5A= 5 + 52 + 53 + .... +5 800 + 5801
5A - A = 5801 - 1
4a = 5801 - 1
5801 - 1 +1 = 5n
⇒ 5801 = 5n ⇒ n = 801

Đề bài thiếu yêu cầu cụ thể em nhé. em cập nhật lại câu hỏi để được sự hỗ trợ tốt nhất cho tài khoản olm vip

A = 5+52+53+.....+52011
A5 = (5+52+53+.....+52011).5
A5 = 52+53+54+.....+52012
A5 - A = (52+53+54+.....+52012)-(5+52+53+.....+52011)
A4 = 52+53+54+.....+52012 - 5-52-53-.....-52011
A4 = 52012 -5
A = (52012 -5) :4
Mà 4A + 5 = 5N => 4 (52012 -5) :4 + 5 = 5N => 52012 -5 + 5 = 5N => 52012 = 5N => N = 52011
\(A=5+5^2+5^3+...+5^{2011}\)
\(5A=\left(5+5^2+5^3+...+5^{2011}\right)\times5\)
\(5A=5^2+5^3+5^4+...+5^{2012}\)
\(5A-A=\left(5^2+5^3+5^4+...+5^{2012}\right)-\left(5+5^2+5^3+....+5^{2011}\right)\)
\(4A=\left(5^2+5^3+5^4+....+5^{2011}\right)-\left(5^2+5^3+5^4+....+5^{2011}\right)+\left(5^{2012}-5\right)\)
\(4A=0+\left(5^{2012}-5\right)=5^{2012}-5\)
\(\Rightarrow4A+5=5^{2012}\)hay \(5^n=5^{2012}\)
\(\Rightarrow n=2012\)

\(A=5^{2016}-5\)
A=132901150760150400933474662701093632444139156230245797983451739952061292318821219082408733380123716446923280138816148691348332250549138432694744733040207471635460062291111714453852983450163412839478432674285466723489853471331344961752024356711039744998722729088056022242066820496791634992123859739046602165056020296822649485842368328334914700117232737216924944154499322138498785527017914889599336202481672782191035035874706832781528727280801652013578429369125463744179027114136759472454584397133928400078670849997607302892223027036473470262496682733564340461161715868386687990733274505753924648948618963125139438987342574828670180634045054186337242659614976824201571903960747675319866959366451316077662320815346287052220792434027927921187356889656584951394657674940726699259495071241216158196484638282891605536718919121672173792307092698308883330916383232492806602360867087932017350554747339691684066271395957046064307027329280820284160155505133882385577240294382888635735834661135764449778633852155557799373087364612366519453980045038199609836307800276035054500661361991243746011829792746699524810528841093775444529181087096473054405737871791062821700667456513545082416389778381211311121521088261300886212326120546085043586116353533714697985212811857529689920199233762425541566473083922473532034610100101045817053433299648552633995654263623546743263019492984489331442211901279648600393556989729404449462890620
b, n = 106320920608120320746779730160874905955311324984196638386761391961649033855056975265926986704098973157538624111052918953078665800439310746155795786432165977308368049832889371563082386760130730271582746139428373378791882777065075969401619485368831795998978183270444817793653456397433307993699087791237281732044816237458119588673894662667931760093786189773539955323599457710799028421614331911679468961985338225752828028699765466225222981824641321610862743495300370995343221691309407577963667517707142720062936679998085842313778421629178776209997346186851472368929372694709350392586619604603139719158895170500111551189874059862936144507236043349069794127691981459361257523168598140255893567493161052862129856652277029641776633947222342336949885511725267961115726139952581359407596056992972926557187710626313284429375135297337739033845674158647106664733106585994245281888693670345613880443797871753347253017116765636851445621863424656227328124404107105908461792235506310908588667728908611559822907081724446239498469891689893215563184036030559687869046240220828043600529089592994996809463834197359619848423072875020355623344869677178443524590297432850257360533965210836065933111822704969048897216870609040708969860896436868034868893082826971758388170249486023751936159387009940433253178467137978825627688080080836653642746639718842107196523410898837394610415594387591465153769521023718880314845591783523559570312500

Lời giải:
a. $(x-3)(y+1)=5=1.5=5.1=(-1)(-5)=(-5)(-1)$
Vì $x-3, y+1$ cũng là số nguyên nên ta có bảng sau:
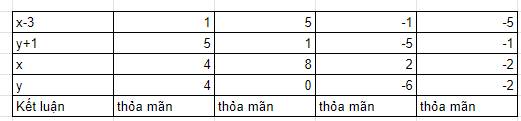
b.
$A=21+5+(5^2+5^3)+(5^4+5^5)+....+(5^{98}+5^{99})$
$=26+5^2(1+5)+5^4(1+5)+....+5^{98}(1+5)$
$=2+24+(1+5)(5^2+5^4+...+5^{98}$
$=2+24+6(5^2+5^4+....+5^{98})=2+6(4+5^2+5^4+...+5^{98})$
$\Rightarrow A$ chia $6$ dư $2$.

\(T=5+5^2+5^3+...+5^{2000}\)
=>\(5T=5^2+5^3+5^4+...+5^{2001}\)
=>\(5T-T=5^2+5^3+...+5^{2001}-5-5^2-...-5^{2000}\)
=>\(4T=5^{2001}-5\)
=>\(4T+5=5^{2001}\)
Sửa đề:\(4T+5=5^m\)
=>\(5^m=5^{2001}\)
=>m=2001
T=5+52+53+...+52000
=>5T=52+53+54+...+52001
=>5T−T=52+53+...+52001−5−52−...−52000
=>4T=52001−5
=>4T+5=52001
Ta có:4T+5=5m
=>52001=5m
=>m=2001
Vậy m=2001

a) \(B=5+5^2+5^3+...+5^{2022}\)
\(\Rightarrow5B=5^2+5^3+5^4+...+5^{2023}\)
\(\Rightarrow4B=5^{2023}-5\)
b) \(4B+5=5^X\)
Hay \(5^{2023}-5+5=5^X\)
\(5^{2023}=5^x\)
\(\Rightarrow x=2023\)
B = 5 + 52 + 53 +...+ 52022
5.B = 52 + 53 +....+ 52023
5B- B = 52023 - 5
4B = 52023 - 5
b, 4B + 5 = 5\(^x\) ⇒ 52023 - 5 + 5 = 5\(^x\)
5\(^{2023}\) = 5\(x\)
\(x\) = 2023


a) \(4n-5⋮13\)
\(\Rightarrow4n-5+13⋮13\Rightarrow4n+8⋮13\Rightarrow4\left(n+2\right)⋮13\)
Vì (4;13) = 1 nên n+2 chia hết cho 13
=> n=13k-2 ( \(k\in N\)*)
b) \(5n+1⋮7\Rightarrow5n+1+14⋮7\Rightarrow5n+15⋮7\Rightarrow5\left(n+3\right)⋮7\)
Vì 5 không chia hết cho 7 nên để 5(n+3) chia hết cho 7 thì n+3 chia hết cho 7
=> n = 7k-3 ( \(k\in N\)*)
c) \(25n+3⋮53\Rightarrow25n+3-53⋮53\Rightarrow25n-50⋮53\Rightarrow25\left(n-2\right)⋮53\Rightarrow n-2⋮53\)
=> n = 53k+2 ( k thuộc N*)

Ta có: A= 5+52+53+...+599 (1)
=> 5A= 52+53+54+...+5100 (2)
Lấy (2)-(1) ta có:
5A-A= ( 52+53+54+...5100) - (5+52+53+...+599)
4A=5100-5
Vì 4A+5=5n
Thay vào ta có: 5100-5+5=5n
5100=5n
=> n=100