Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\frac{1}{3}x-\frac{3}{5}=\frac{5}{6}x+2\)
\(\Leftrightarrow\frac{x}{3}-\frac{3}{5}=\frac{5x}{6}+2\)
\(\Leftrightarrow2x-\frac{18}{5}=5x+12\)
\(\Leftrightarrow2x-5x=\frac{18}{5}+12\)
\(\Leftrightarrow-3x=\frac{78}{5}\)
\(\Leftrightarrow3x=-\frac{78}{5}\)
\(\Leftrightarrow x=-\frac{26}{5}\)
Ps: đoạn nào không hiểu hỏi anh nhé. Nhớ k để tạo động lực cho anh nhé :33
# Aeri #

2:
a: =>-3/4-x=-1/2
=>x=-3/4+1/2=-3/4+2/4=-1/4
b: =>x^2=36
=>x=6 hoặc x=-6
c: =>x-9/20=-5/12
=>x=-5/12+9/20=1/30
d: x+-3/4=-11/3
=>x=-11/3+3/4=-35/12
e: =>1/3:x=4/3+5/3=3
=>x=1/9

Vì 7x8y chia hết cho 2 và 5
Nên y chỉ có thể là 0
Nếu y là 0 thì (7 + x + 8 + 0) chia hết cho 9
<=> 15 + x chia hết cho 9
<=> x = 3
Vậy số ần tìm là 7380

a) Giả sử `(x+1)^2 >= 4x` là đúng.
Có: `(x+1)^2 >=4x <=> x^2+2x+1>=4x`
`<=>x^2+1>=2x`
`<=>x^2-2x+1>=0`
`<=> (x-1)^2>=0 forall x`.
Vậy điều giả sử là đúng.
b) `x^2+y^2+2 >=2(x+y)`
`<=> (x^2-2x+1)+(y^2-2y+1) >=0`
`<=>(x-1)^2+(y-1)^2>=0 forall x,y`
c) `(1/x+1/y)(x+y)>=4`
`<=> (x+y)/(xy) (x+y) >=4`
`<=> (x+y)^2 >= 4xy`
`<=> x^2+2xy+y^2>=4xy`
`<=> (x-y)^2>=0 forall x,y > 0`
d) `x/y+y/x>=2`
`<=> (x^2+y^2)/(xy) >=2`
`<=> x^2+y^2 >=2xy`
`<=> (x-y)^2>=0 \forall x,y>0`.
a) Xét hiệu \(\left(x+1\right)^2-4x\) = \(x^2-2x+1=\left(x-1\right)^2\ge0\)
=> \(\left(x+1\right)^2-\text{4x}\) \(\ge\) 0
=> \(\left(x+1\right)^2\ge\text{4x}\) (điều phải chứng minh)
b) xét hiệu \(x^2+y^2+2-2\left(x+y\right)\) = \(\left(x-1\right)^2+\left(y-1\right)^2\ge0\)
=> \(x^2+y^2+2-2\left(x+y\right)\ge0\)
=> \(x^2+y^2+2\ge2\left(x+y\right)\) (điều phải chứng minh)
c) Xét hiệu \(\left(\dfrac{1}{x}+\dfrac{1}{y}\right)\left(x+y\right)-4\) = \((\dfrac{x+y}{xy})\left(x+y\right)-4=\dfrac{\left(x+y\right)^2-4xy}{xy}=\dfrac{\left(x-y\right)^2}{xy}\) \(\ge0\)(vì x>0,y>0)
=>\(\left(\dfrac{1}{x}+\dfrac{1}{y}\right)\left(x+y\right)\ge4\) (điều phải chứng minh)
d) Áp dụng bất đẳng thức Cau-Chy cho các số x>0;y>0 ta có
\(\dfrac{x}{y}+\dfrac{y}{x}\ge2.\left(\dfrac{xy}{yx}\right)=2\)
=> \(\dfrac{x}{y}+\dfrac{y}{x}\ge2\) (điều phải chứng minh)
Mình làm hơi tắt mong bạn thông cảm nhé
Chúc bạn học tốt


a) \(x^2-2x+1-y^2=\left(x-1\right)^2-y^2=\left(x-1-y\right)\left(x-1+y\right)\)
b)\(=\left(x+y\right)^2-z^2=\left(x+y+z\right)\left(x+y-z\right)\)
mấy ý còn lại tương tự nha
a,\(x^2-y^2+1-2x\)
\(=\left(x-1\right)^2-y^2\)
\(=\left(x-1+y\right)\left(x-1-y\right)\)
\(b,x^2+2xy-z^2+y^2\)
\(=\left(x+y\right)^2-z^2\)
\(=\left(x+y+z\right)\left(x+y-z\right)\)
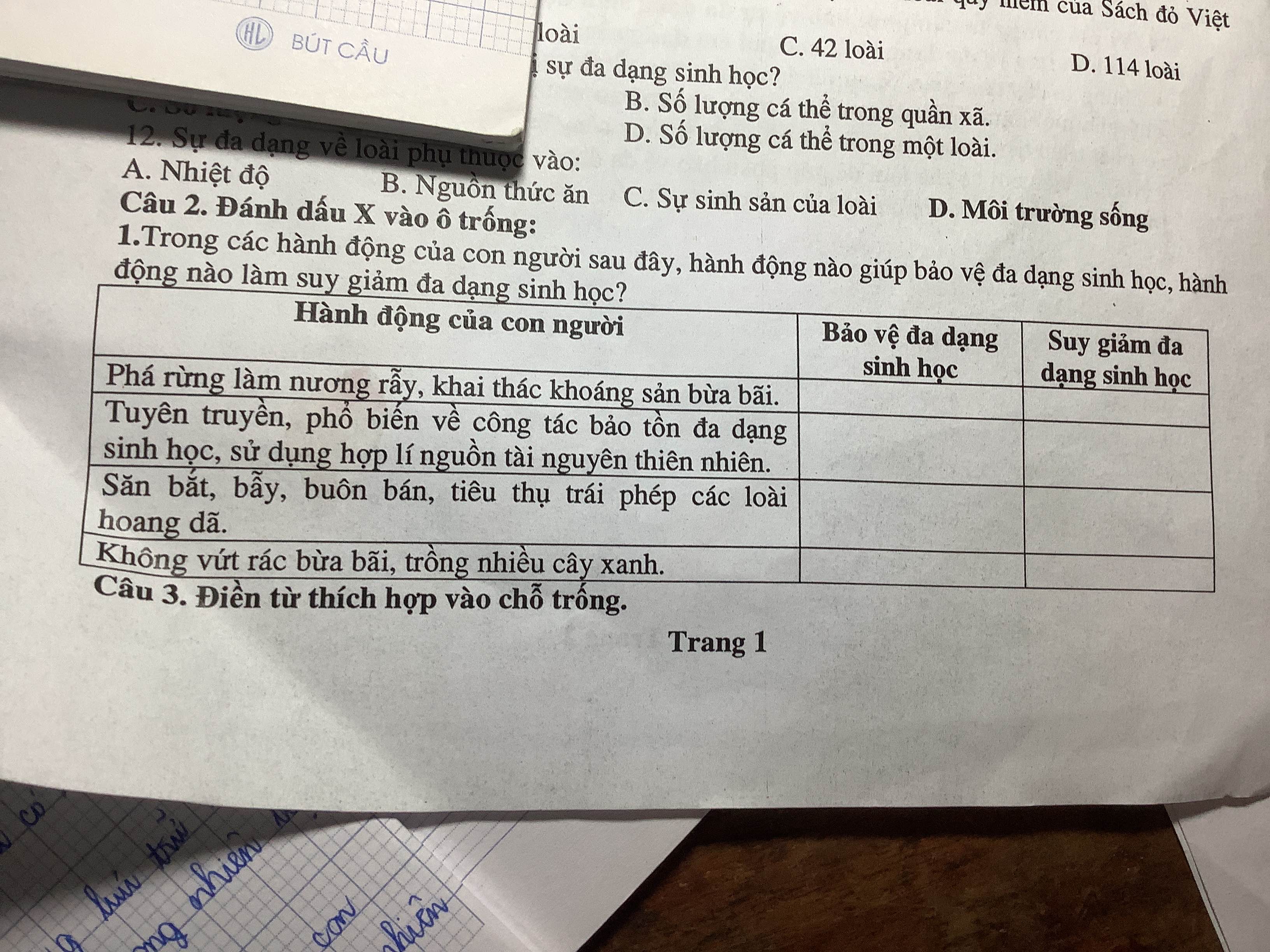 Giúp mik câu 2 vs ạ.Thanks❣️Môn Nội dung giáo dục địa phương
Giúp mik câu 2 vs ạ.Thanks❣️Môn Nội dung giáo dục địa phương
x^2 + x + 1 >0
\(x^2+x+1>0\\\Rightarrow x^2+x+\frac{1}{4}+\frac{3}{4}>0\\ \Rightarrow\left(x+\frac{1}{2}\right)^2>-\frac{3}{4}\left(ĐPCM\right)\)
\(x^2+x+1=\left[x^2+2.x.\frac{1}{2}+\left(\frac{1}{2}\right)^2\right]+1-\left(\frac{1}{2}\right)^2\)\(=\left(x+\frac{1}{2}\right)^2+\frac{3}{4}\)
Mà \(\left(x+\frac{1}{2}\right)^2\ge0\Rightarrow\left(x+\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}>0\)