cho hai góc kề bù xoy và yoz . biet xoy = 2 yoz
tính yoz
vẽ tia oy' là tia đối của tia oy , tính góc xoy'
viết tên các cặp góc đối đỉnh
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 10 2016
a) góc xOy và góc yOz kề bù (GT)
=> góc xOy + góc yOz = 180 độ (t/c)
Mà góc xOy = 2 . góc yOz (GT)
=> 2 . góc yOz + góc yOz = 180 độ (t/c bắc cầu)
3 . góc yOz = 180 độ
góc yOz = 60 độ (1)
b) xOy và yOz là 2 góc kề bù (GT)
=> Ox và Oz đối nhau
xOy' và yOz là 2 góc đối đỉnh (do Oy và Oy' đối nhau; Ox và Oz đối nhau)
=> góc xOy' = góc yOz (2)
Từ (1) và (2) => góc xOy' = 60 độ (t/c bắc cầu)
c) Các cặp góc đối đỉnh: xOy' và yOz; xOy và y'Oz
13 tháng 10 2015
Ta có xOy + yOz = 180o (kề bù)
Mà xOy = 2yOz <=> \(\frac{xOy}{2}=\frac{yOz}{1}=\frac{xOy+yOz}{2+1}=\frac{180^o}{3}=60^o\)
=> xOy = 60o . 2 = 120o
yOz = 60o . 1 = 60o
21 tháng 10 2016
Ta có hình vẽ:
a) Ta có: xOy + yOz = 180o (kề bù)
=> 2.yOz + yOz = 180o
=> 3.yOz = 180o
=> yOz = 180o : 3 = 60o
b) Có: xOy = 2.yOz = 2.60o = 120o
c) Vì xOy và yOz là 2 góc kề bù nên Ox và Oz là 2 tia đối nhau
Mà Oy' và Oy là 2 tia đối nhau
Như vậy, các cặp góc đối đỉnh là: xOy và zOy'; zOy và xOy'
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
14 tháng 9 2023
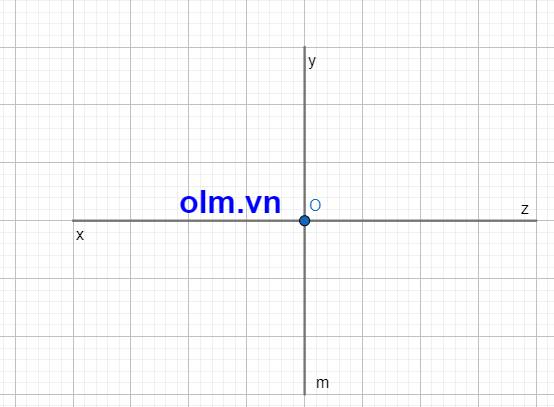
a, \(\widehat{xOy}\) + \(\widehat{yOz}\) = 1800; \(\widehat{xOy}\) = \(\widehat{yOz}\) ⇒ 2\(\widehat{xOy}\) = 1800
⇒ \(\widehat{yOz}\) = \(\widehat{xOy}\) = 1800 : 2 = 900
b, Các cặp góc bằng nhau là:
\(\widehat{yOz}\) = \(\widehat{xOm}\); \(\widehat{yOz}\) = \(\widehat{xOy}\); \(\widehat{yOz}\) = \(\widehat{zOm}\);
\(\widehat{zOm}\) = \(\widehat{mOx}\); \(\widehat{zOm}\) = \(\widehat{xOz}\);
\(\widehat{xOm}\) = \(\widehat{xOy}\);
11 tháng 7 2019
a) Ta có : yOx + yOz = 180°
Mà 3yOz = xOy
=> 3yOz + yOz = 180°
=> 4yOz = 180°
=> yOz = 180 : 4 = 45°
=> xOy = 180 - 45 = 135°
b) Vì Oy' là tia đối Oy'
=> yOz = xOy' = 45°
=> yOx = zOy' = 135°
23 tháng 9 2017
a.
=> xOy+yOz=180'
=>2yOz+yOz=!80'
=>3yOz=180'
=>yOz=180':3
=>yOz=60'
b.
=>xOy'=yOz=60'(2 góc đối đỉnh)
c.
Các cặp góc đối đỉnh trong hình là: xOy' và yOz, y'Oz và xOy
23 tháng 9 2017
bài của mình thiếu 2 góc kề bù ỏ phần giải thích câu a bạn sửa lại giùm nha!