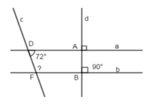
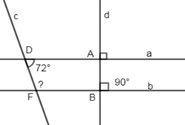
dfb asws swde
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì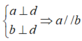 (quan hệ giữa tính vuông góc và tính song song)
(quan hệ giữa tính vuông góc và tính song song)
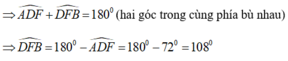
Chọn đáp án D.

a, Theo định lí Pytago tam giác DHE vuông tại H
\(EH=\sqrt{DE^2-DH^2}=\dfrac{27}{5}cm\)
-> HF = 15 - 27/5 = 48/5 cm
Theo định lí Pytago tam giác DHF vuông tại H
\(DF=\sqrt{DH^2+HF^2}=12\)cm
b, Ta có \(EF^2=DE^2+DF^2\Rightarrow225=81+144\)(luôn đúng)
Vậy tam giác DEF vuông tại D

a: Xét ΔAOE và ΔCOF có
\(\widehat{EAO}=\widehat{FCO}\)
OA=OC
\(\widehat{AOE}=\widehat{COF}\)
Do đó: ΔAOE=ΔCOF
Suy ra: AE=CF
Ta có: AE+EB=AB
CF+FD=CD
mà AB=CD
và AE=CF
nên EB=FD
b: Ta có: ΔAOE=ΔCOF
nên OE=OF
mà O nằm giữa E và F
nên O là trung điểm của EF

a: DH=căn DE^2-EH^2=12cm
Xét ΔDEF vuông tại D có DH là đường cao
nên DE^2=EH*EF
=>EF=15^2/9=25cm
DF=căn 25^2-15^2=20cm
HF=25-9=16cm
b: C=15+20+25=40+20=60cm
S=1/2*15*20=10*15=150cm2
DM=EF/2=25/2=12,5cm
c: Xét ΔEDF có HK//DF
nên HK/DF=EH/EF
=>HK/20=9/25
=>HK=180/25=7,2cm

Theo định lí Pytago tam giác DEF vuông tại D
\(DF=\sqrt{EF^2-DE^2}=16cm\)
b, Xét tam giác EDF và tam giác DHF
^DFE _ chung
^EDF = ^DHF = 900
Vậy tam giác EDF ~ tam giác DHF (g.g)
\(\dfrac{EF}{DF}=\dfrac{DF}{HF}\Rightarrow DF^2=EF.HF\)
a: \(DF=\sqrt{20^2-12^2}=16\left(cm\right)\)
b: Xét ΔEDF vuông tại D và ΔDHF vuông tại H có
góc F chung
Do đó: ΔEDF\(\sim\)ΔDHF

a: DF=4cm
b: Xét ΔFEK có
FD là đường cao
FD là đường trung tuyến
Do đó: ΔFEK cân tại F
c: Xét ΔFIG và ΔEID có
\(\widehat{FIG}=\widehat{EID}\)
IF=IE
\(\widehat{IFG}=\widehat{IED}\)
Do đó: ΔFIG=ΔEID
Suy ra: GF=DE=3cm
d: Xét tứ giác DGFK có
FG//DK
FG=DK
Do đó: DGFK là hình bình hành
Suy ra: DF và GK cắt nhau tại trung điểm của mỗi đường
mà Q là trung điểm của DF
nên Q là trung điểm của GK
hay G,Q,K thẳng hàng
a, Theo định lí Pytago tam giác DEF vuông tại D
\(DF=\sqrt{FE^2-DE^2}=4cm\)
b, Xét tam giác EKF có :
DF là đường cao
Lại có : D là trung điểm EK
=> FD đồng thời là đường trung tuyến
Vậy tam giác EFK cân tại F
c, thiếu đề