viết phương trình mặt cầu (S) có tâm I (3;-4;2) và tiếp xúc với mặt phẳng OXY
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CK
1
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 3 2023
Do (S) tiếp xúc Oxy \(\Rightarrow R=\left|z_I\right|=2\)
Phương trình (S):
\(\left(x-3\right)^2+\left(y+4\right)^2+\left(z-2\right)^2=4\)
CM
18 tháng 11 2017
Chọn C
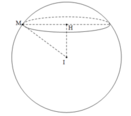
Ta có h = d(I, (P)) = 1
Gọi (C) là đường tròn giao tuyến có bán kính r.
Vì S = r2.π = 2π <=> r = √2
Mà R2 = r2 + h2 = 3 => R = √3
Vậy phương trình mặt cầu tâm i (0; -2; 1) và bán kính R = √3
CM
28 tháng 6 2018
Đáp án B
Mặt cầu (S’) đối xứng với mặt cầu (S) qua gốc tọa độ nên mặt cầu (S’) có tâm I’(-1;-2; 1) đối xứng với I qua gốc O và có bán kính R’ = R = 3.
Phương trình mặt cầu (S’) là: ( x + 1 ) 2 + ( y + 2 ) 2 + ( z - 1 ) 2 = 9
CM
13 tháng 4 2017
Đáp án C.
Ta có I ∈ O y ⇒ I 0 ; i ; 0 , i > 0.
O x z : y = 0 ⇒ d I ; O x z = R = 4 ⇔ i 4 = 4 ⇒ i = 4 ⇒ I 0 ; 4 ; 0 ⇒ x 2 + y − 4 + z 2 = 16.
CM
14 tháng 3 2019
Đáp án B
Ta có: bán kính mặt cầu tâm I tiếp xúc với mặt phẳng ( α ) là khoảng cách từ I đến mặt phẳng
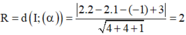
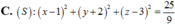
Khoảng cách từ điểm I(3;-4;2) đến mp(Oxy) bằng \(\left|y_I\right|=\left|-4\right|=4\).
Vậy bán kính của mặt cầu (S) bằng 4, ta có phương trình:
\(\left(x-3\right)^2+\left(y+4\right)^2+\left(z-2\right)^2=4^2\).