
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




`#3107.101107`
`4.`
`a.`
mZn + mHCl = mZnCl\(_2\) + mH\(_2\)
`b.`
`@` Theo định luật bảo toàn khối lượng
\(m_{Zn}+m_{HCl}=m_{ZnCl_2}+m_{H_2}\)
`=>`\(26+\text{HCl}=54,4+0,8\)
`=>`\(\text{HCl}=54,4+0,8-26\)
`=>`\(\text{HCl}=55,2-26\)
`=>`\(\text{HCl}=29,2\left(g\right)\)
Vậy, khối lượng của HCl trong pứ trên là `29,2` g.

2:
a: A(x)=0
=>-5x+3=0
=>-5x=-3
=>x=3/5
b: B(x)=0
=>2x^3-18x=0
=>2x(x^2-9)=0
=>x(x-3)(x+3)=0
=>x=0;x=3;x=-3
c: C(x)=0
=>-x(-x-5)=0
=>x(x+5)=0
=>x=0 hoặc x=-5
d: D(x)=0
=>3x-3+2x^2-2x-x^2+2x-1=0
=>x^2+3x-4=0
=>x=-4 hoặc x=1
e: E(x)=0
=>2x^3-2x-x^2+1=0
=>2x(x^2-1)-(x^2-1)=0
=>(2x-1)(x-1)(x+1)=0
=>x=1/2;x=-1;x=1

Bạn gõ hẳn đề ra thì khả năng mọi người sẽ giúp bạn sẽ cao hơn nhé. Đọc như thế này hơi khó.

{nhận xét về bài làm của bạn}
bạn ơi là phép tính có nhớ bạn ạ
[ lời giải ]
* ngôi nhà số 1 ( kết quả là 12) ( phép cộng )
- 5 + 7
- 6 + 6
- 4 + 8
- 9 + 3
* ngôi nhà số 2 ( kết quả là 4 ) ( phép trừ )
- 11 - 7
- 12 - 8
- 13 - 9
- 10 - 6
* ngôi nhà sồ 3 (kết quả là 5 ) ( phép trừ )
- 13 - 8
- 12 - 7
- 11 - 6
- 10 - 5
[giải thích (hoặc là hướng dẫn) cách làm]
- bạn chỉ cần tạo ra 1 phép tính có nhớ trong phạm vi 20
- mỗi ngôi nhà có kết quả và mẫu phép tính
- bạn cần đọc và hiểu mẫu đề bài cho rồi tự làm
Đáp án : sai. 6-2 không phải là phép tính có nhớ còn nhiều lỗi lắm

Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}a+b=2\\-3a+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=\dfrac{3}{2}\end{matrix}\right.\)

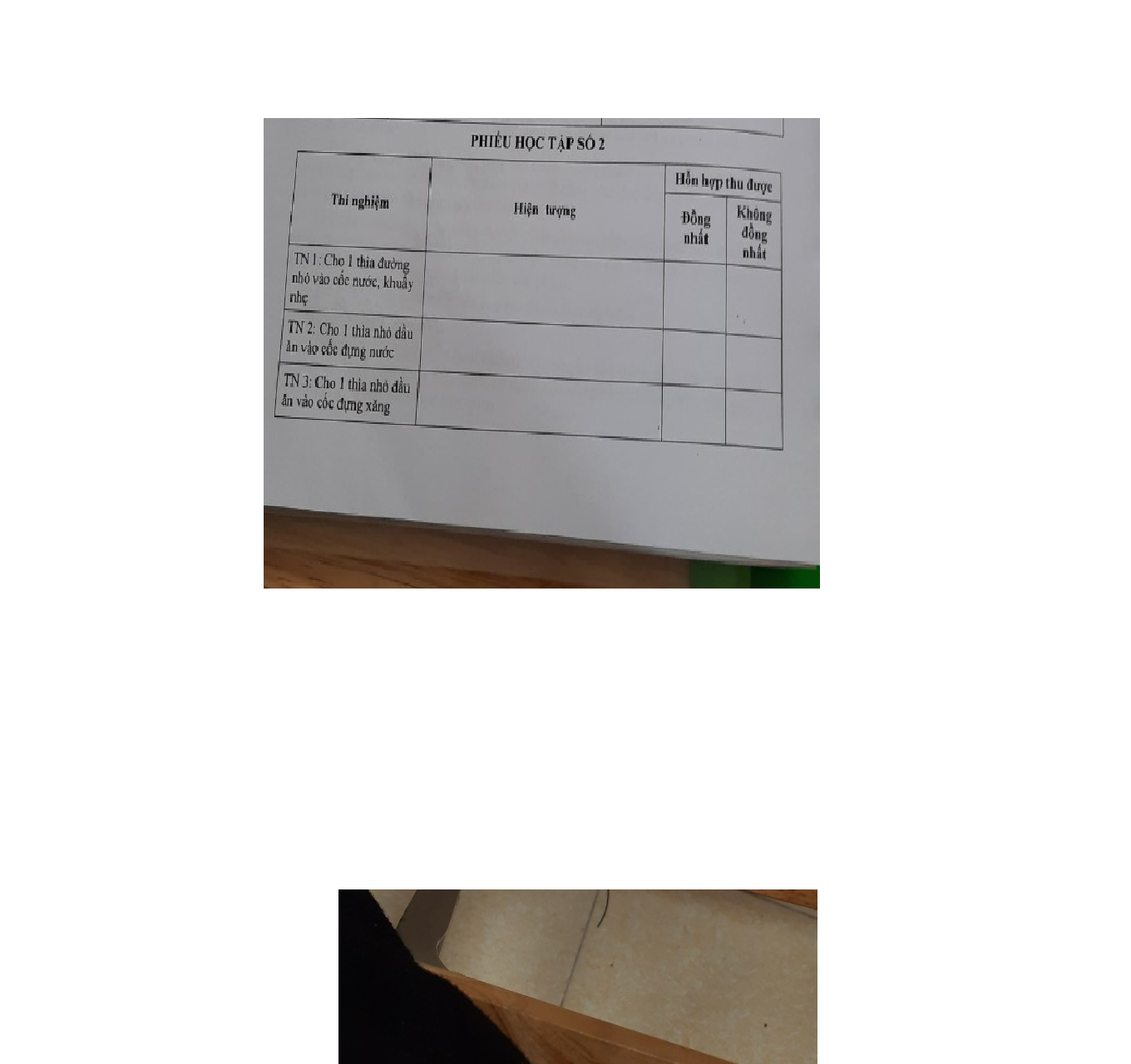


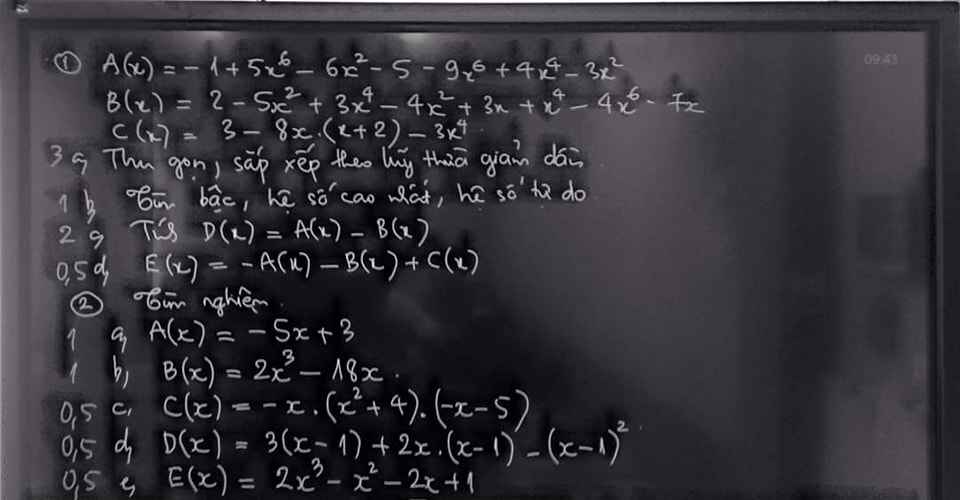
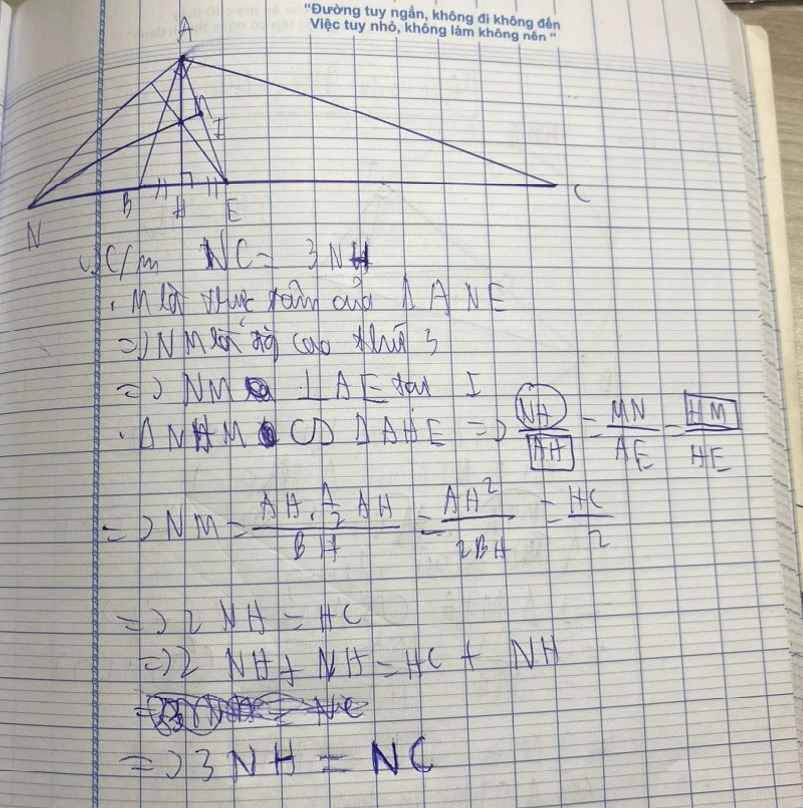 bạn nào có thể làm giúp mình bài này theo những ý như này được không ạ
bạn nào có thể làm giúp mình bài này theo những ý như này được không ạ cho mình hỏi bài 5 này làm như nào ạ, mình làm như thế đã đúng chưa
cho mình hỏi bài 5 này làm như nào ạ, mình làm như thế đã đúng chưa
a, Thay x = 36 vào B ta được : \(B=\frac{6}{6-3}=\frac{6}{3}=2\)
b, \(B< \frac{1}{2}\Leftrightarrow\frac{\sqrt{x}}{\sqrt{x}-3}-\frac{1}{2}< 0\Leftrightarrow\frac{\sqrt{x}+3}{2\left(\sqrt{x}-3\right)}< 0\)Với \(x>0;x\ne9\)
\(\Rightarrow\sqrt{x}-3< 0\Leftrightarrow x< 9\Rightarrow0< x< 9\)
c, Với \(x>0;x\ne1\)
\(A=\left(\frac{\sqrt{x}}{\sqrt{x}-1}-\frac{1}{x-\sqrt{x}}\right):\frac{\sqrt{x}+1}{\sqrt{x}+2}\)
\(=\left(\frac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right):\frac{\sqrt{x}+1}{\sqrt{x}+2}=\frac{\sqrt{x}+2}{\sqrt{x}}\)
d, \(P=AB=\frac{\sqrt{x}+2}{\sqrt{x}-3}=\frac{\sqrt{x}-3+5}{\sqrt{x}-3}=1+\frac{5}{\sqrt{x}-3}\)
\(\Rightarrow\sqrt{x}-3\inƯ\left(5\right)=\left\{\pm1;\pm5\right\}\)