cho hàm số y= f(x)=\(\dfrac{1}{2}x\)
a, tính f(x0;f(-6);f(\(1\dfrac{3}{4}\) )
b, xác định các cặp số (x;y)tương ứng vừa tính
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
11 tháng 9 2021
Lời giải:
a. Tại $x_0=\sqrt{5}$ thì:
$y=f(x_0)=\frac{x_0}{2}-\sqrt{x_0^2-1}+2$
$=\frac{\sqrt{5}}{2}-\sqrt{5-1}+2=\frac{\sqrt{5}}{2}$
b. Tại $x=\frac{1}{4}$ thì $x^2-1=\frac{-15}{16}< 0$ nên căn thức $\sqrt{x^2-1}$ không xác định. Do đó không tính được.
21 tháng 10 2023
a: \(f\left(\dfrac{1}{2}\right)=\left(\dfrac{1}{2}\right)^2+\dfrac{1}{2}-2=\dfrac{1}{4}+\dfrac{1}{2}-2=\dfrac{3}{8}-2=\dfrac{3-16}{8}=-\dfrac{13}{8}\)
b: \(f\left(\sqrt{3}\right)=\dfrac{2\sqrt{3}}{\left(\sqrt{3}\right)^2+1}=\dfrac{2\sqrt{3}}{4}=\dfrac{\sqrt{3}}{2}\)
CM
30 tháng 11 2017
Đáp án A
Phương pháp:
Dựa vào khái niệm cực trị và các kiến thức liên quan.
Cách giải:
(1) chỉ là điều kiện cần mà không là điều kiện đủ.
VD hàm số y = x3 có y' = 3x2 = 0 ⇔ x = 0. Tuy nhiên x = 0 không là điểm cực trị của hàm số.
(2) sai, khi f''(x0) = 0, ta không có kết luận về điểm x0 có là cực trị của hàm số hay không.
(3) hiển nhiên sai.
Vậy (1), (2), (3): sai; (4): đúng
HG
1
TA
22 tháng 11 2023
1,Thay x = 1 vào biểu thức ta có
f = 4 x 12 -5
f = -1
2, Đặt f(x) = -1, ta có:
4 x x2 - 5 = -1
4 x x2 = 4
x2 = 4 : 4
x2 = 1
x2=12
=> x = 1 hoặc = -1
Vậy để f(x)=1 thì x ϵ {-1;1}
CM
26 tháng 10 2019
Đặt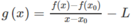 
Suy ra g(x) xác định trên
(
a
;
b
)
\
x
0
và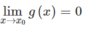 
Mặt khác, f ( x ) = f ( x 0 ) + L ( x − x 0 ) + ( x − x 0 ) g ( x ) nên
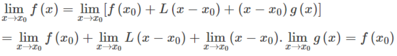
Vậy hàm số y = f(x) liên tục tại
27 tháng 8 2021
c: Ở hai hàm số trên, nếu lấy biến x cùng một giá trị thì f(x) sẽ nhỏ hơn g(x) 3 đơn vị
CM
16 tháng 9 2017
Số 2 lớn hơn mọi giá trị khác của hàm số f(x) = sinx với tập xác định D = R nhưng 2 không phải là giá trị lớn nhất của hàm số này (giá trị lớn nhất là 1); vì vậy A sai. Cũng như vậy B sai với f(x) = sinx, D = R, M = 2. Phát biểu C tự mâu thuẫn: vì M = f( x 0 ), x 0 ∈ D nên hay không xảy ra M > f(x), ∀x ∈ D.
Đáp án: D
a: f(0)=0
f(-6)=-3
f(7/4)=7/8
b: \(\left(x,y\right)\in\left\{\left(0;0\right);\left(-6;-3\right);\left(\dfrac{7}{4};\dfrac{7}{8}\right)\right\}\)