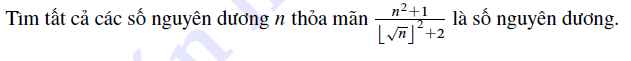
Làm hộ em bài này với ạ
P/s: [\(\sqrt{n}\)]\(^2\) là (phần nguyên của \(\sqrt{n}\))\(^2\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Viết lại đẳng thức cần cm
\(1^3+2^3+..+n^3=\left(1+2+..+n\right)^2\)(*)
với n =1 thì \(1^3=1^2\)(ĐÚNG )
với n=2 thì \(1^3+2^3=9=3^2\)(ĐÚNG)
Giả sử (*) đúng với \(n=k\left(k\in N,k\ne0\right)\Leftrightarrow1^3+2^3+..+k^3=\left(1+2+..+k\right)^2\)
Ta đi chứng minh (*) đúng với n=k+1
Thạt vậy \(1^3+2^3+..+k^3+\left(k+1\right)^3=\left(1+..+k\right)^2+\left(k+1\right)^3\)
\(=\left(1+..+k\right)^2+\left(k+1\right)\left(k+1\right)^2=\left(1+..+k\right)^2+k\left(k+1\right)^2+\left(k+1\right)^2\)
\(=\left(1+..+k\right)^2+2\left(k+1\right)\left(1+..+k\right)+\left(k+1\right)^2=\left(1+..+k+k+1\right)^2\)(dpcm )

n là số nguyên dương
Bình phương hai vế, ta được:
\(\left(\sqrt{n+2}-\sqrt{n+1}\right)^2=n+2+n+1-2\sqrt{\left(n+2\right)\left(n+1\right)}\) \(=2n+3-2\sqrt{\left(n+2\right)\left(n+1\right)}\)
\(\left(\sqrt{n+1}-\sqrt{n}\right)^2=n+1+n-2\sqrt{n\left(n+1\right)}\) \(=2n+1-2\sqrt{n\left(n+1\right)}\)
Ta có: \(\left(n+2\right)\left(n+1\right)>n\left(n+1\right)\Rightarrow2\sqrt{\left(n+2\right)\left(n+1\right)}>2\sqrt{n\left(n+1\right)}\)
Mà 2n + 3 > 2n + 1
\(\Rightarrow2n+3-2\sqrt{\left(n+2\right)\left(n+1\right)}>2n+1-2\sqrt{n\left(n+1\right)}\)
=> ( √n+2 - √n+1)^2 > ( √n-1 - √n)^2
=> √n+2 - √n+1 > √n-1 - √n
P/s: Em làm còn sai nhiều, mong mọi người góp ý, đừng chọn sai cho em. Em cảm ơn

4. \(\sqrt{x}+\sqrt{y}=6\sqrt{55}\)
\(6\sqrt{55}\) là số vô tỉ, suy ra vế trái phải là các căn thức đồng dạng chứa \(\sqrt{55}\)
Đặt \(\sqrt{x}=a\sqrt{55};\sqrt{y}=b\sqrt{55}\) với \(a,b\in N\)
\(\Rightarrow a+b=6\)
Xét các TH:
a = 0 => b = 6
a = 1 => b = 5
a = 2 => b = 4
a = 3 => b = 3
a = 4 => b = 2
a = 5 => b = 1
a = 6 => b = 0
Từ đó dễ dàng tìm đc x, y

n2 + 6n = n(n + 6) chia hết n
Mà n2 + 6n phải là số nguyên tố => n = 1
Thử lại: n(n + 6) = 7 nguyên tố
Vậy n = 1

Ta có:
Áp dụng bất đẳng thức Cauchy cho k + 1 số ta có:
Lần lượt cho k = 1, 2, 3, ... rồi cộng lại ta được