Chứng minh rằng :
Nếu (a2- bc)(b - abc) = (b2 - ac)(a - abc) và các số a,b,c; a-b#0 thì \(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=a+b+c\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
2
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 9 2021
Kẻ đường cao BD ứng với AC. Do góc A tù \(\Rightarrow\) D nằm ngoài đoạn thẳng AC hay \(CD=AD+AC\) và \(\widehat{DAB}=180^0-120^0=60^0\)
Áp dụng định lý Pitago:
\(AB^2=BD^2+AD^2\) \(\Rightarrow BD^2=AB^2-AD^2\)
Trong tam giác vuông ABD:
\(cos\widehat{BAD}=\dfrac{AD}{AB}\Rightarrow\dfrac{AD}{AB}=cos60^0=\dfrac{1}{2}\Rightarrow AD=\dfrac{1}{2}AB\)
\(\Rightarrow BD^2=AB^2-\left(\dfrac{1}{2}AB^2\right)=\dfrac{3}{4}AB^2\)
Pitago tam giác BCD:
\(BC^2=BD^2+CD^2=\dfrac{3}{4}AB^2+\left(AD+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\left(\dfrac{1}{2}AB+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\dfrac{1}{4}AB^2+AB.AC+AC^2\)
\(=AB^2+AB.AC+AC^2\)
Hay \(a^2=b^2+c^2+bc\)
HP
27 tháng 8 2021
Giả sử \(c\le1\).
Khi đó: \(ab+bc+ca-abc=ab\left(1-c\right)+c\left(a+b\right)\ge0\)
\(\Rightarrow ab+bc+ca\ge abc\left(1\right)\)
Đẳng thức xảy ra chẳng hạn với \(a=2,b=c=0\).
Theo giả thiết:
\(4=a^2+b^2+c^2+abc\ge2ab+c^2+abc\)
\(\Leftrightarrow ab\left(c+2\right)\le4-c^2\)
\(\Leftrightarrow ab\le2-c\)
Trong ba số \(\left(a-1\right),\left(b-1\right),\left(c-1\right)\) luôn có hai số cùng dấu.
Không mất tính tổng quát, giả sử \(\left(a-1\right)\left(b-1\right)\ge0\).
\(\Rightarrow ab-a-b+1\ge0\)
\(\Leftrightarrow ab\ge a+b-1\)
\(\Leftrightarrow abc\ge ca+bc-c\)
\(\Rightarrow abc+2\ge ca+bc+2-c\ge ab+bc+ca\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\Rightarrow\) Bất đẳng thức được chứng minh.
6 tháng 1 2022
a: \(\Leftrightarrow\left(a+1\right)^2-4a\ge0\)
hay \(\left(a-1\right)^2>=0\)(luôn đúng)
b: \(VT=a^2c^2+2abcd+b^2d^2+a^2d^2-2abcd+b^2c^2\)
\(=a^2\left(c^2+d^2\right)+b^2\left(c^2+d^2\right)\)
\(=\left(c^2+d^2\right)\left(a^2+b^2\right)=VP\)
HN
1
20 tháng 8 2023
Ta có :
\(\left(a-b-c\right)^2=a^2+b^2+c^2-2ab-2bc-2ac\)
mà theo đề bài \(a^2+b^2+c^2-ab-bc-ac=0\)
\(\Rightarrow\left(a-b-c\right)^2=-ab-bc-ac=0\)
\(\Rightarrow\left(a-b-c\right)^2=-\left(ab+bc+ac\right)=0\)
mà \(-\left(ab+bc+ac\right)\le0\)
\(\Rightarrow a=b=c=0\)
\(\Rightarrow dpcm\)
CM
3 tháng 4 2019
Trong tam giác ABC, theo Hệ quả định lý Cô sin ta luôn có :
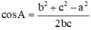
Mà ta có 2.bc > 0 nên cos A luôn cùng dấu với b2 + c2 – a2.
a) Góc A nhọn ⇔ cos A > 0 ⇔ b2 + c2 – a2 > 0 ⇔ a2 < b2 + c2.
b) Góc A tù ⇔ cos A < 0 ⇔ b2 + c2 – a2 < 0 ⇔ a2 > b2 + c2.
c) Góc A vuông ⇔ cos A = 0 ⇔ b2 + c2 – a2 = 0 ⇔ a2 = b2 + c2.
Có :
\(\left(a^2-bc\right)\left(b-abc\right)=\left(b^2-ac\right)\left(a-abc\right)\)
\(\Leftrightarrow ab\left(a-b\right)+c\left(a^2-b^2\right)=abc^2\left(a-b\right)+abc\left(a^2-b^2\right)\)
\(\Leftrightarrow a^2b-a^3bc-b^2c+ab^2c^2=ab^2-ab^3c-a^2c+a^2bc^2\)
\(\Leftrightarrow ab\left(a-b\right)+c\left(a-b\right)\left(a+b\right)=abc^2\left(a-b\right)+abc\left(a-b\right)\left(a+b\right)\)
\(\Leftrightarrow\left(a-b\right)\left(ab+ac+bc\right)=abc\left(a-b\right)\left(a+b+c\right)\)
Chia 2 vế cho abc(a-b) khác 0 ta được :
\(\left(ab+ac+bc\right):abc=a+b+c\)
\(\Leftrightarrow\dfrac{ab}{abc}+\dfrac{bc}{abc}+\dfrac{ac}{abc}=a+b+c\)
\(\Leftrightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=a+b+c\left(đpcm\right)\)