Biết các cạnh của một tam giác tỉ lệ với 2;3;4 và chu vi của nó là 45cm. Tính các cạnh của tam giác đó.
{ AI BIẾT HỘ MIK VỚI GHI CÁCH GIẢI CHI TIẾT NHA }
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) bạn sai đề rồi phải tỉ lệ với 2;4;5 cơ mik làm rồi hjhj
gọi độ dài các cạnh đó lần lượt là a;b;c
=>a/2=b/4=c/5
áp dug t/c dãy t/s = nhua ta có:
a/2=b/4=c/5=a+b+c/2+4+5=22/11=2
=>a/2=2=>a=4
=>b/4=2=>b=8
=>c/5=2=>c=10

a: Gọi độ dài ba cạnh lần lượt là a,b,c
Theo đề, ta có: a/4=b/5=c/7 và a+b+c-2a=2
Áp dụng tính chất của DTBSN, ta được:
\(\dfrac{a}{4}=\dfrac{b}{5}=\dfrac{c}{7}=\dfrac{a+b+c-2a}{4+5+7-2\cdot4}=\dfrac{2}{8}=\dfrac{1}{4}\)
=>a=1; b=5/4; c=7/4
b: Gọi độ dài ba cạnh lần lượt là a,b,c
Theo đề, ta có:
a/2=b/4=c/5
Áp dụng tính chất của DTSBN, ta đc:
\(\dfrac{a}{2}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{2+4+5}=\dfrac{33}{11}=3\)
=>a=6; b=12; c=15

Gọi chiều dài của các cạnh của tam giác tỉ lệ với 2 ,3 ,4 (cm) lần lượt là x ,y ,z
Các cạnh của tam giác tỉ lệ với 2, 3, 4 nghĩa là x : 2 = y : 3 = z : 4, hay 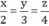
Chu vi tam giác bằng 45 nghĩa là x + y+ z = 45
Theo tính chất của dãy tỉ số bằng nhau ta có 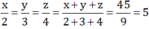
Do đó x = 5.2 = 10 ; y = 5.3 = 15 ; z = 5.4 = 20
Vậy các cạnh của tam giác là 10cm ; 15cm ; 20cm

Gọi độ dài các cạnh của tam giác lần lượt là x, y, z (cm)
Theo đề bài ta có x + y + z = 36 và
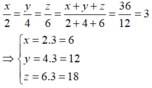
Chọn đáp án B

Giải
Gọi chiều dài của các cạnh của tam giác tỉ lệ với 2 ,3 ,4 (cm) lần lượt là x ,y ,z
Các cạnh của tam giác tỉ lệ với 2, 3, 4 nghĩa là x : 2 = y : 3 = z : 4, hay \(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}\)
Chu vi tam giác bằng 45 nghĩa là x + y+ z = 45
Theo tính chất của dãy tỉ số bằng nhau ta có \(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=\frac{x+y+z}{2+3+4}=\)45/9 \(=5\)
Do đó x = 5.2 = 10 ; y = 5.3 = 15 ; z = 5.4 = 20
Vậy các cạnh của tam giác là 10cm ; 15cm ; 20cm

Bài 4:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{2}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{2+4+5}=\dfrac{44}{11}=4\)
Do đó: a=8; b=16; c=20

Ta có hình vẽ:
A B C
Ta có sơ đồ:
Cạnh AB: |----------|
Cạnh BC: |----------|----------|
Cạnh CA: |----------|----------|----------|
Tổng số phần bằng nhau là:
1 + 2 + 3 = 6 ( phần )
Cạnh AB dài:
45 : 6 x 1 = 7, 5 ( cm )
Cạnh BC dài:
45 : 6 x 2 = 15 ( cm )
Cạnh CA dài:
45 : 6 x 3 = 22, 5 ( cm )
Đáp số: ...
~ Chúc bạn học tốt ~
Tổng số phần bằng nhau là :
2 + 3 + 4 = 9 ( phần )
Cạnh AB là :
45 : 9 x 2 = 10 ( cm )
Cạnh BC là :
45 : 9 x 3 = 15 ( cm )
Cạnh CA là :
45 : 9 x 4 = 20 ( cm )
Đ/S : ...............

Gọi chiếu dài (cm) của các cạnh của tam giác tỉ lệ với 2, 3, 4 lần lượt là x, y, z.
Theo đề bài, ta có:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}\)và x + y + z = 45
Theo tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{x}{2}= \frac{y}{3}= \frac{z}{4} = \frac{x + y + z}{2 + 3 + 4 } = \frac{45}{9} = 5 \)
Nên x = 5.2 = 10
y = 5.3 = 15
z = 5.4 = 20
Vậy các cạnh của tam giác là 10cm, 15cm, 20cm.
Gọi chiếu dài (cm) của các cạnh của tam giác tỉ lệ với 2, 3, 4 lần lượt là x, y, z.
Theo đề bài, ta có:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}\)và x + y + z = 45
Theo tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{x}{2}= \frac{y}{3}= \frac{z}{4} = \frac{x + y + z}{2 + 3 + 4 } = \frac{45}{9} = 5 \)
Nên x = 5.2 = 10
y = 5.3 = 15
z = 5.4 = 20
Vậy các cạnh của tam giác là 10cm, 15cm, 20cm.
Gọi độ dài các cạnh của tam giác đó lần lượt là a, b, c.
Theo đề ta có:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}\) và \(a+b+c=45\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+b+c}{2+3+4}=\dfrac{45}{9}=5\)
\(\dfrac{a}{2}=5\Rightarrow a=5.2=10\)
\(\dfrac{b}{3}=5\Rightarrow b=5.3=15\)
\(\dfrac{c}{4}=5\Rightarrow c=5.4=20\)
Vậy các độ cạnh của tan giác đó lần lượt là 10cm, 15cm, 20cm.
Gọi 3 cạn của tam giác đó lần lượt là a,b,c
Theo bài ta có :
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}\)
\(a+b+c=45\left(cm\right)\)
Áp dụng t,c dãy tỉ số bằng nhau ta có :
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+b+c}{2+3+4}=\dfrac{45}{9}=5\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{a}{2}=5\\\dfrac{b}{3}=5\\\dfrac{c}{4}=5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=10\\b=15\\c=20\end{matrix}\right.\)
Vậy ..